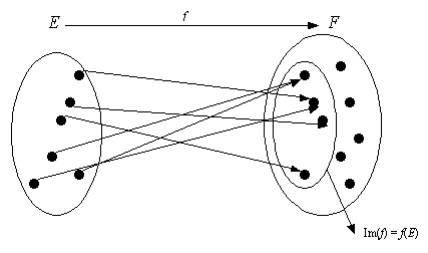
Soit f : E ® F une application linéaire. L’ensemble des images des éléments de E, , est un sous-espace vectoriel de F appelé image de l’application linéaire f et noté .

Remarque
- est une partie de F :
- La dimension de est appelée rang de f : .
Soit f : E ® F une application linéaire. Alors est un espace-vectoriel.
Soit f : E ® F. L’ensemble défini par est un sous-espace vectoriel de E appelé noyau de l’application linéaire f.
(ker = kernel qui veut dire noyau en anglais).
Remarque
est une partie de E : .
Exemple 2 (
![]() très
important)
très
important)
Soit définie par :
.
Déterminer et . Réponse.