Les matrices
4
Déterminants
4.1
Formes multilinéaires alternées
On rappelle que .
Définition 1
·       Soit E un espace vectoriel. Une application de
 est une application multilinéaire ou n‑linéaire si elle est linéaire par rapport à chacune de ses variables :
(i)Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Soit
 tel que
. Alors :
                      Â
(ii)Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Soit
 tel que
 avec
. Alors :
                      Â
·       Si
, on dit que D est une forme n‑linéaire.
Définition 2
Soit E un espace vectoriel et
 une forme n-linéaire. On dit que D est alternée
si
 chaque fois que deux des
 sont identiques :
                      Â
 dès que
 pour
4.2 Déterminant
d’un système de vecteurs
Théorème
Il existe une unique application
 telle que :
(i)                 D est une forme n-linéaire ;
(ii)               D est alternée ;
(iii)Â Â Â Â Â Â Â Â Â Â Â Â Â Â
 où les
 sont les vecteurs de la base canonique de
.
Définition
Cette application
 n-linéaire alternée et telle que
 est appelée déterminant. On la note généralement det.
Remarque
Soit
 une famille de vecteurs
,
. Alors
 et
.
4.3 Déterminant
d’une matrice carrée
Soit A une
matrice carrée d’ordre n. Soit
.
Chaque colonne de A peut alors être considérée comme un vecteur de
:
 avec
 pour
Ainsi, la
définition de la notion de déterminant d’une matrice carrée est étroitement
liée à la définition du déterminant d’un système de vecteurs :
On note alors
,
et on par le de déterminant d’ordre n.
La suite du chapitre traite du calcul pratique des déterminants.
4.3.1
Déterminant d’une matrice carrée d’ordre 2
Définition
Soit
. Alors
.
Moyen mnémotechnique
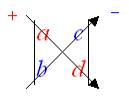
Exemple 8
Soit
.
Calculer
.
Réponse.
4.3.2
Déterminant d’une matrice carrée d’ordre 3
Règle
de Sarrus
 Cette règle n’est valable que pour des
matrices carrées d’ordre 3, et n’est absolument pas généralisable. Mieux vaut
donc lui préférer la règle générale énoncée dans le paragraphe suivant.
Soit
.
                                                         Â
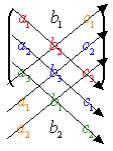
Exemple 9
Soit
.
Calculer
 par
la règle de Sarrus. Réponse.
4.3.3
Généralisation : Déterminant d’ordre n
Méthode des cofacteurs
L’astuce consiste à se ramener à des déterminants d’ordre
inférieur jusqu’à obtenir des déterminants d’ordre 2. Pour cela, on développe
le déterminant par rapport à une ligne ou une colonne.
Soit
 un déterminant d’ordre n.
,
développement par rapport à la ligne i
,
développement par rapport à la colonne j
où
 est le cofacteur
de l’élément
:
 est le mineur
de
 c’est-à -dire le déterminant d’ordre
 extrait de
 en enlevant la ième ligne
et la jème colonne.
Application :
 (ligne 1)
 (colonne 1)
             Â
Remarque
La répartition des signes à prendre devant les mineurs
, est alternée à partir du signe + pour l’élément
.
Par exemple, pour un déterminant d’ordre 5 :
+Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +
-Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -
+Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +
-Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -
+Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +Â Â Â Â Â Â Â Â Â -Â Â Â Â Â Â Â Â Â +
Application au déterminant d’ordre 3
 (colonne 1)
Exemple 10
Calculer le déterminant suivant
,
avec la méthode des cofacteurs. Réponse.
Propositions
a)     ® Si A a une ligne (ou une colonne) de zéros alors
® Si A a deux lignes (ou deux colonnes) identiques alors
b)     Si on échange deux lignes (deux colonnes) d’un déterminant alors on obtient
 et
c)     On ne modifie pas un déterminant si on ajoute à une ligne (resp. une colonne) une combinaison linéaire des autres lignes (resp. des autres colonnes) :
d)     Si on multiplie une ligne (resp. une colonne) d’un déterminant par un scalaire
, alors le déterminant est lui-même multiplié par
.
e)Â Â Â Â Â Si
 est une matrice triangulaire d’ordre n alors
 (produit des termes diagonaux). Il en résulte que
.
Exemple :
f)Â Â Â Â Â Â Â
 ®
Le déterminant est une fonction multiplicative.
g)Â Â Â Â Â
h)Â Â Â Â Â
i)Â Â Â Â Â Â Â
Exemple 11 (propositions b et c)
Soit
.
Vérifier les propositions b et c précédentes. Réponse.
4.4
Déterminant et volume
Les déterminants sont liés aux aires et aux volumes. Soient
 des vecteurs de
.
Soit S le parallélépipède (solide) déterminé par ces
vecteurs :
Lorsque
,
S est un parallélogramme.
Soit
 le volume de S (ou la surface de S
dans le cas
 ). Alors :
Si on appelle A la matrice dont les colonnes
correspondent aux vecteurs
,
alors :
Proposition
 si et seulement si les vecteurs
 sont linéairement dépendants.