D’après l’inégalité de Cauchy-Schwartz, , et donc l’angle existe toujours et est unique.
Représentation graphique
Si est un produit scalaire sur un espace vectoriel E, pour tout :
ce qui équivaut à
Remarque
Le symbole désigne la valeur absolue.
Soit E un espace préhilbertien. Alors la norme de E satisfait les propriétés suivantes :
(i) et
(ii)
(iii)
Remarque
La propriété (iii) est appelée « inégalité triangulaire » car si on considère comme troisième côté du triangle formé avec et , alors (iii) signifie que la longueur d’un côté du triangle est inférieure ou égale à la somme des longueurs des deux autres côtés.
Soit E un espace préhilbertien. Soit . Si , ou si de manière équivalente , alors est appelé un vecteur unitaire.
Si un vecteur quelconque de E espace préhilbertien, alors le vecteur est unitaire et colinéaire à . On appelle le vecteur normé associé à . Le procédé correspondant s’appelle la normalisation.
Remarque
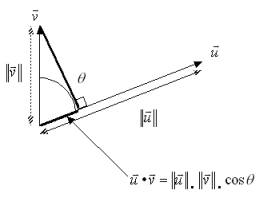
Quels que soient les vecteurs , l’angle que font entre eux les vecteurs et est l’angle tel que et :
D’après l’inégalité de Cauchy-Schwartz, , et donc l’angle existe toujours et est unique.
Représentation graphique
