Fonctions – Généralités

5         Variation des fonctions

5.1         Fonctions croissantes, décroissantes, monotones

Définitions :

Soit .

·        On dit que f est croissante sur I si ,   .

·        On dit que f est décroissante sur I si ,   .

·        On dit que f est strictement croissante sur I si ,   .

·        On dit que f est strictement décroissante sur I si ,   .

·        On dit que f est (strictement) monotone sur I si elle est (strictement) croissante ou (strictement) décroissante sur I.

 

Exemple :

Considérons la fonction définie sur  par .

Montrer que la fonction f est strictement décroissante sur  et strictement croissante sur .                                                                          Réponse

5.2       Somme et produit de fonctions monotones

Définition :

Soit . On dit que f est positive (respectivement négative), si ,  (respectivement  ).

 

Propositions : Soient  et .

(i)            Si f et g ont même monotonie, alors  est monotone de même monotonie.

Si de plus f ou g est strictement monotone, alors  est strictement monotone.

(ii)          Si f et g sont positives croissantes, alors  est positive croissante ;

Si f et g sont positives décroissantes, alors  est positive décroissante.

(iii)         Si f et g sont négatives croissantes, alors  est positive décroissante ;

Si f et g sont négatives décroissantes, alors  est positive croissante.

(iv)        Si f est positive croissante et g négative décroissante, alors  est négative décroissante ;

Si f est positive décroissante et g négative croissante, alors  est négative croissante.

 

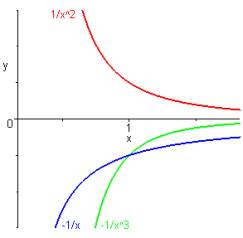
Exemple :

Soit f définie par  positive décroissante sur  (voir proposition suivante) et g définie par  négative croissante sur . Alors  est négative croissante sur .

 

Remarques :

·                    Cas d’indétermination sur le produit de deux fonctions :

 

f

g

fg

Positive croissante

Positive décroissante

?

Positive décroissante

Négative décroissante

?

Positive croissante

Négative croissante

?

Négative croissante

Négative décroissante

?

 

·                    Si , alors  et f ont même monotonie ;

·                    Si , alors  et f sont de monotonie contraire ; c’est le cas de  et f.

 

5.3       Inverse d’une fonction monotone

Proposition :

Soit  monotone. Si on suppose que f ne s’annule jamais sur I, et qu’elle est de signe constant, alors la fonction inverse  est monotone sur I, de monotonie contraire à celle de f et de même signe.

 

Exemples :

(1)    On retrouve le résultat de l’exercice précédent en prenant .

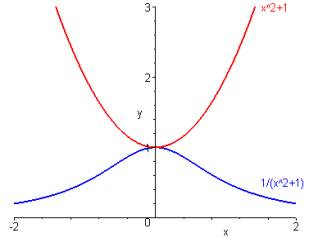
(2)    Soit la fonction f définie par . f est positive strictement croissante sur  et ne s’y annule jamais. Par conséquent,  est strictement décroissante sur . On peut faire le même raisonnement sur .

5.4       Composition de fonctions monotones

Proposition :

Soient deux fonctions, f définie sur un intervalle  et g définie sur un intervalle , telles que   .

(i)                  Si f et g ont même monotonie, l’une sur I et l’autre sur J, alors la composée  est croissante sur I.

(ii)                Si f et g sont de monotonie contraire, l’une sur I et l’autre sur J, alors la composée  est décroissante sur I.

 

Démonstration

 

Exemple :

Soit la fonction h définie sur l’intervalle  par .

Montrer que la fonction h est croissante sur , et décroissante sur . Réponse