Dérivation – Etude de fonctions

7         Convexité

On rappelle que dans ce chapitre I est un intervalle ouvert de .

7.1      Définitions

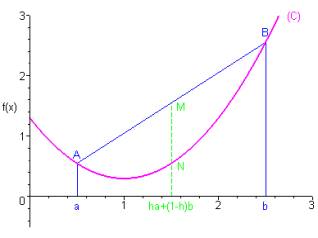
Une fonction est dite convexe si son graphe à la forme suivante : courbe (C).

 

 

Les coordonnées des différents points de la courbe sont :

avec

La convexité de f signifie que pour tout , l’ordonnée de N est inférieure ou égale à celle de M.

Lorsque h décrit , N parcourt l’arc , tandis que M parcourt la corde .

Ainsi, dire que f est convexe signifie que pour tous les points de la courbe entre A et B, la corde  est « au-dessus » de l’arc .

 

Définition :

 est dite convexe sur I si et seulement si :

, ,

 

Exemples 18

 

Propositions 1 :

(1)       tels que ,

  (Inégalité des trois points)

(2)       ,  définie par  est croissante.

Ces propositions sont équivalentes à la définition.

 

Définition 2 :

 est dite concave si  est convexe.

 

Exemple :

La fonction définie sur  par  est concave. Voir graphe précédent.

 

Proposition 2 :

Les fonctions affines définies sur  par , dont la courbe représentative est une droite, sont à la fois convexes et concaves sur .

 

Démonstration

 

Proposition 3 :

Soient , , …,  des fonctions définies de I dans , et convexes sur I. Alors tous strictement positifs, la fonction  définie de I dans , est aussi convexe.

 

7.2      Critères de convexités

Proposition 4 (caractérisation de la convexité par la dérivée première) :

Soit  dérivable. Alors f est convexe si et seulement si  est croissante sur I.

 

Conséquence (tangente à la courbe d’une fonction convexe) :

Soit  dérivable et convexe. Alors pour tout , on a :

            ,

Autrement dit, la courbe représentative de f est partout au-dessus des tangentes.

 

Exemple 19

 

Proposition 5 (caractérisation de la convexité par la dérivée seconde) :

Soit  deux fois dérivable. Alors f est convexe si et seulement   .

 

Exemple :

Considérons à nouveau la fonction définie sur  par .

 sur  tout entier.

 

Définition 3 :

Soient  deux fois dérivable et , différent des bornes. On dit que  est un point d’inflexion si  s’annule et change de signe au point  ;

On dit que la courbe représentative de f « traverse » la tangente au point .

 

Exemple 20