Définition 2 :
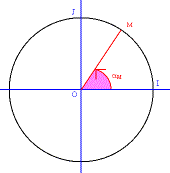
Soit M un point du cercle trigonométrique. On appelle mesure en radians de l’angle , le réel égal à la longueur de l’arc orienté (de I vers M).
D’après le site de L. Garnier (Université de Bourgogne)
On considère un repère orthonormé , c’est-à-dire tel que et .
Définitions 1 :
Le cercle trigonométrique est le cercle de centre O et de rayon 1 sur le quel on définit un sens de parcours.
Le sens est positif est le sens inverse des aiguilles d’une montre : on dit le sens trigonométrique direct.
Le sens est négatif est le sens des aiguilles d’une montre : c’est le sens trigonométrique indirect.
Remarque : Ces définitions ne sont en fait par rigoureuses au sens mathématique, puisque le sens trigonométrique direct ne peut en théorie être défini que dans .
Définition 2 :
Soit M un point du cercle trigonométrique. On appelle mesure en radians de l’angle , le réel égal à la longueur de l’arc orienté (de I vers M).

D’après le site de L. Garnier (Université de Bourgogne)
Remarque :
Si M et N ont même position sur le cercle trigonométrique, alors avec .
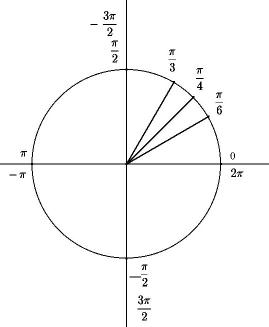
Le graphe ci-dessous donne quelques valeurs remarquables d’angles :
D’après le site de L. Garnier (Université de Bourgogne)
Définitions 3 :
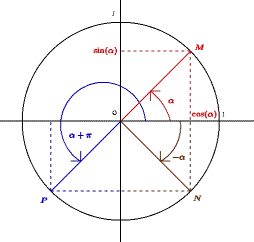
Soit M un point du cercle trigonométrique.
On appelle sinus de l’angle l’ordonnée du point M.
On appelle cosinus de l’angle l’abscisse du point M.
D’après le site de L. Garnier (Université de Bourgogne)
Pour tout angle , on a les relations suivantes (voir graphe ci-dessus) :
|
, ,
|
|
Vous trouverez une liste d’autres relations dans l’aide mémoire « trigonométrie ».
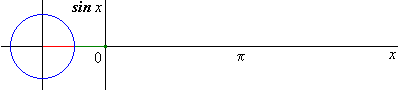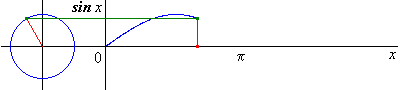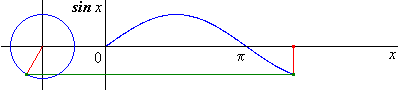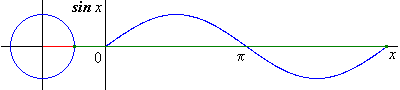
Du latin sinus = pli, cavité J
Elle est définie sur par
Elle est impaire et -périodique.
Elle est dérivable sur avec .
Elle est strictement croissante sur et strictement décroissante sur .
Sa courbe est une sinusoïde ; elle est invariante par :
- les translations de vecteur (puisqu’elle est -périodique)
- les symétries de centres (puisqu’elle est impaire)
- les symétries d’axes
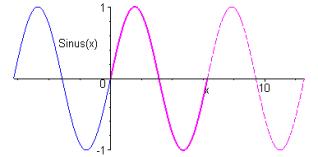
Version animée :
 D’après le site de X. Hubaut
(Université de Bruxelle)
D’après le site de X. Hubaut
(Université de Bruxelle)
du latin cum = avec donnant en français co = associé et sinus = pli
Elle est définie sur par
Elle est paire et -périodique.
Elle est dérivable sur avec .
Elle est strictement croissante sur et strictement décroissante sur .
Sa courbe est une sinusoïde ; elle est invariante par :
- les translations de vecteur
- les symétries de centres
- les symétries d’axes
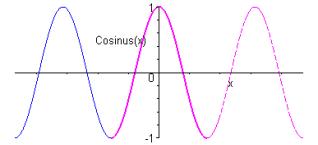
du latin tangere, tangentis = toucher
Elle est définie sur par
Elle est impaire et -périodique.
Elle est dérivable sur avec .
Elle est strictement croissante sur
Sa courbe est invariante par :
- les translations de vecteur
- les symétries de centres
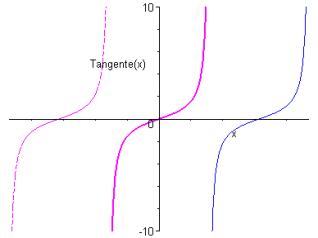
du latin cum = avec donnant en français co = associé et tangente
Elle est définie sur par
Elle est impaire et -périodique.
Elle est dérivable sur avec .
Elle est strictement décroissante sur
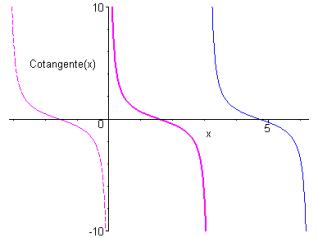
La fonction sinus est bijective de tout intervalle vers ; elle admet donc une fonction réciproque définie de vers
Ainsi, pour tout il existe un unique tel que .
Par définition, ce nombre y est appelé arc sinus x, et noté .
Elle est par construction définie, continue et impaire sur .
Son graphe est symétrique de celui de sinus par symétrie par rapport à la première bissectrice.
Sa dérivée se calcule selon la règle établie au chapitre 3 §4.4 pour les fonctions réciproques :
Elle est donc strictement croissante sur avec deux tangentes verticales en 1 et .
Représentation graphique de la fonction arcsinus
(par un raisonnement analogue au précédent)
Elle est définie, continue et paire sur .
Son graphe se déduit de celui de cosinus par symétrie par rapport à la première bissectrice.
Sa dérivée se calcule comme précédemment :
Elle est donc strictement décroissante sur avec deux tangentes verticales en 1 et .
Représentation graphique de la fonction arccosinus
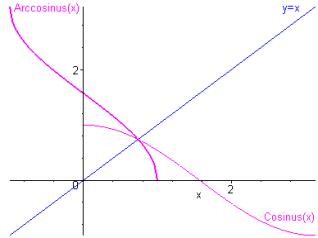
Elle est définie, continue et impaire sur .
Son graphe se déduit de celui de tagente par symétrie par rapport à la première bissectrice.
Sa dérivée se calcule comme précédemment :
La fonction arctangente est donc strictement croissante sur .
Représentation graphique de la fonction arctangente
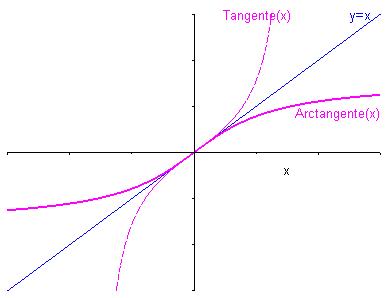
Relations fondamentales :
avec
Les formules de Simpson et bien d’autres sont répertoriées dans le formulaire « trigonométrie » de la rubrique aide-mémoire. On les utilise pour transformer des sommes de sinus ou de cosinus en produits de sinus ou de cosinus. Ces formules trouvent des applications pour la calcul intégral (voir Chapitre 5).
Vers d’autres applications des formules de Simpson…
A l’aide des théorème de fonctions composées, il est facile d’obtenir les propriétés de fonctions s’écrivant comme combinaison des fonctions trigonométriques précédentes. Ainsi :
Les variations de température dans l’eau du Rhône sont cycliques, dépendent de la saison, et sont directement liées aux variations cycliques de la dureté de l’eau, mesurée en mg/L de CaC03 (carbonate de calcium).
Par exemple, on peut imaginer la relation suivante, si t désigne le temps et D la dureté de l’eau:
t est dite variable de contrôle (sa variation influence celle de D) ;
D est dite variable dépendent (ses variations dépendent de celles de t) ;
sont des paramètres, dont les valeurs dépendent de l’endroit et/ou du moment où sont mesurées les variations de D. Les valeurs de ces paramètres peuvent aussi varier d’une année à l’autre, voire d’une saison à l’autre.
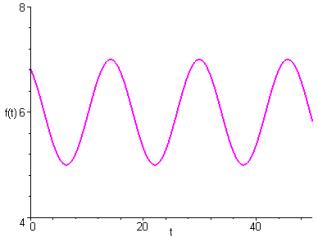
f est définie sur ; elle est -périodique.
La représentation graphique d’une telle fonction, pour des valeurs quelconques des paramètres est la suivante :
Des mesures de D ont été effectuées sur une durée totale d’un an (Carrel G., 1986) :
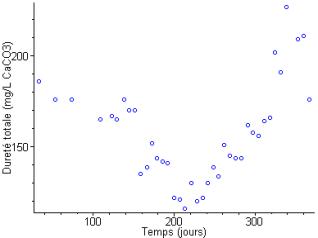
De telles mesures étant réalisées, il peut-être intéressant de savoir quelle fonction f permet de décrire l’évolution de la dureté de l’eau dans le temps. Il s’agit alors de trouver les valeurs des paramètres telles que la courbe représentative de passe « au mieux » entre les points. On parle dans ce cas d’ajustement d’une courbe (ou d’un modèle) à des données expérimentales.
Une telle analyse est possible à l’aide des logiciels Maple ou R et donne les résultats suivants :
|
|
|
15873 : un site dédié aux mathématiques utilitaires de tous niveaux, sous forme d'exercices avec leurs solutions. Avec une partie "Aide Mémoire" (formulaire) pour les choses courantes.
Voir le formulaire trigo