Primitives – Intégration
5 Méthodes de calcul approché d’intégrales
Lorsque la primitive de ne peut pas être calculée de façon simple, ou que cela demande des calculs trop longs, on est alors amené à calculer de manière approchée à l’aide d’une méthode numérique.
Nous présentons dans ce paragraphe les méthodes graphiques les plus classiques.
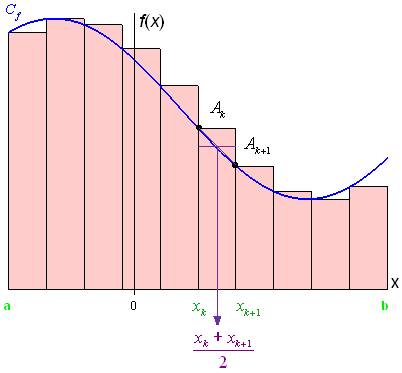
Soit f une fonction positive et intégrable sur un intervalle et sa courbe représentative ; On cherche une valeur approchée de .
L’idée de départ, commune aux méthodes graphiques qui vont nous intéresser, est que l’on partage l’intervalle d’intégration en n intervalles égaux de longueur , avec et .
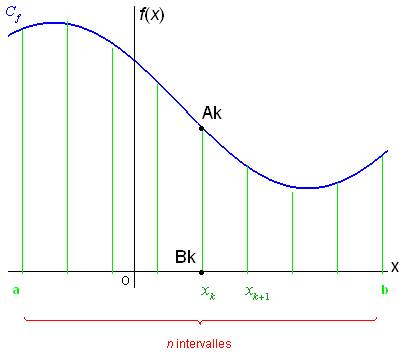
Les points ont pour coordonnées ;
Les points ont pour coordonnées .
On désigne par une approximation de la fonction f sur les intervalles .
Ainsi, on peut décomposer en avec . On prend alors comme valeur approchée de : .
Le choix de la fonction conduit à l’une des trois méthodes présentées ci-dessous.
5.1 Méthode des rectangles
Cette méthode est directement inspirée de la définition des intégrales.
On prend comme fonction , la fonction constante qui correspond à la valeur de f au point milieu de l’intervalle .
Ainsi, on a .
La valeur approchée de I est alors donnée par (voir figure ci-dessous) :