Définition 1 :
On appelle équation différentielle une relation entre les valeurs de la variable x et les valeurs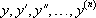 
d’une fonction inconnue et de ses dérivées au point x.
Définition 1 :
On appelle équation différentielle une relation entre les valeurs de la variable x et les valeurs 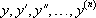d’une fonction inconnue et de ses dérivées au point x.
On rappelle que :
- 
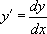désigne la dérivée première de la fonction y par rapport à sa variable x ;
- 
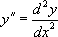désigne la dérivée seconde de la fonction y par rapport à sa variable x ;
- 
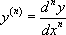désigne la dérivée n-ième de la fonction y par rapport à sa variable x.
On dit que l’équation différentielle est d’ordre n si elle contient la dérivée n-ième de y, et pas celles d’ordre supérieur :
- 
: 
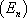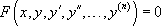est une équation différentielle d’ordre n
- 
: 
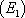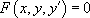est une équation différentielle d’ordre 1
- 
: 
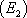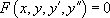est une équation différentielle d’ordre 2
Définition 2 :
Une solution d’une équation différentielle est une fonction f continue et dérivable (jusqu’à l’ordre n pour une équation d’ordre n) dans un intervalle I donné, et telle que pour toute valeur x de I, les valeurs de f et de ses dérivées vérifient l’équation.
Par exemple, la fonction f est une solution de l’équation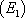 
si :
, 
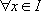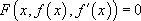
La fonction f est une solution de l’équation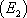 
si :
, 
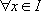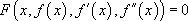
Définitions 3 :
· La courbe représentative de la solution d’une équation différentielle est une chronique ou courbe intégrale.
· Résoudre ou intégrer une équation différentielle c’est trouver toutes ses solutions.
L’équation différentielle la plus simple est l’équation :
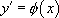
Remarques :
· Les solutions de cette équation sont les primitives de la fonction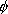 
; mais si pour une fonction 
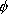continue nous savons que ces primitives existent, nous ne pouvons pas toujours en donner une expression simple à l’aide des fonctions élémentaires.
· Une équation différentielle admet une infinité de solutions (c’est le cas en particulier de l’équation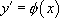 
). Pour trouver la solution particulière du problème étudié, il faut tenir compte des conditions particulières (ou conditions initiales) que doit satisfaire la solution. Ainsi pour une équation du premier ordre comme 
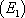, la condition initiale sera en général que la solution f prend la valeur 
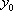en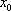 
: 
.
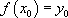Exemple :
Considérons l’équation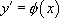 
.
Soit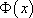 
la primitive de 
.
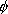Les solutions de l’équations sont donc les fonctions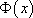 
, et il n’existe qu’une seule solution particulière telle que 
.
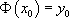Application :
Soit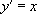 
. Alors 
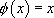avec ses primitives 
.
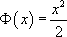Les solutions sont donc les fonctions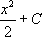 
avec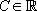 
une constante.
Pour chercher la solution particulière telle que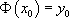 
on écrit :
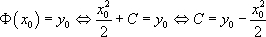
Ainsi, la solution particulière recherchée est la fonction définie par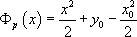 
.