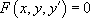.Les équations différentielles d’ordre 1, on dit aussi du premier ordre, ne font intervenir que des dérivées premières : .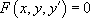
La forme générale de ces équations est :
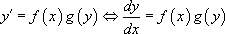
Ainsi, on peut écrire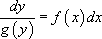 
, ce qui revient à calculer deux primitives :
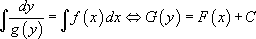avec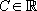 
une constante
Exemples :
« Résoudre l’équation  |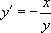
|
« Résoudre l’équation  |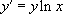
|
« Résoudre l’équation  |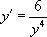
La forme générale de ces équations est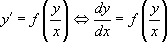 
.
L’astuce consiste à poser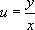 
pour se ramener à une équation à variables séparables.
On pose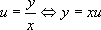 
Ainsi,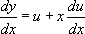 
(u est en effet une fonction de x), c’est-à-dire :
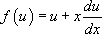
Ceci qui permet alors d’écrire :
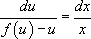
On est donc bien ramené au cas précédent.
Exemples :
« Résoudre l’équation  |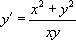
|
« Résoudre l’équation  |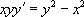
Cherchons à décrire au moyen d’une équation différentielle l’évolution de la taille de la population d'un pays qui présente les caractéristiques suivantes : par an, le taux de renouvellement est de 20 pour 1000 habitants, et le taux de mortalité est de 15 pour 1000 habitants.
Soit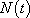 
la taille de la population l’année t, exprimée en milliers d’habitants.
La variation annuelle de la taille de la population peut être quantifiée à l’aide de la quantité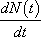 
. Ainsi, on peut écrire, par le jeu d’une balance entre renouvellement naturel et mortalité :
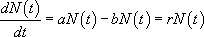
avec :
- a le taux de renouvellement de la population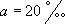 
;
- b le taux de mortalité de la population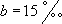 
;
- r le taux d’accroissement absolu de la population :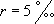 
.
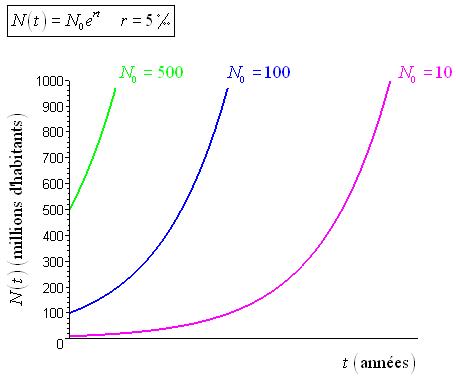
Pour connaître l’évolution de N en fonction de t, il faut maintenant résoudre :
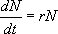
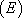
Il s’agit d’une équation différentielle à variable séparable qui s’intègre simplement :
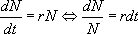
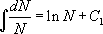
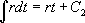
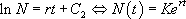
La valeur de K dépend de la condition initiale choisie. Si on suppose que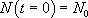 
, il vient :
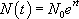
Voici la représentation graphique de la relation N en fonction de t pour différentes valeurs de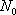 
:
