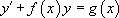.Une équation différentielle linéaire d’ordre 1 est de la forme .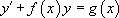
On parle d’équation différentielle linéaire d’ordre 1 sans second membre si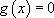 
(SSM).
On parle d’équation différentielle linéaire d’ordre 1 avec second membre si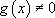 
(ASM).
La fonction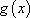 
est le second membre de l’équation. L’équation SSM est encore appelée équation homogène.
Nous considérons dans ce paragraphe des équations de la forme :
: 
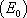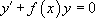
Ces équations SSM sont à variables séparables et aisément intégrables sous réserve de pouvoir calculer la primitive de la fonction f :
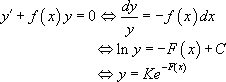
Exemples :
« Résoudre l’équation  |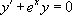
|
|
« Résoudre l’équation |
Nous considérons dans ce paragraphe des équations de la forme :
: 
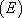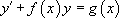
Ces équations ASM se résolvent en deux temps :
(1) On intègre d’abord l’équation SSM pour obtenir :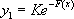 
(2) On résout l’équation ASM, soit en recherchant une solution particulière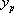 
de 
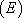(voir § 3.2.1), soit en utilisant la méthode de variation de la constante (voir § 3.2.2).
Supposons que l’on dispose d’une solution particulièr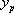e 
de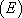 
, alors la solution générale de 
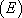est la fonction définie par 
.
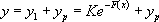Vérification :
Soit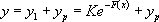 
. Montrons qu’une telle fonction est bien solution de 
.
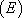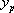est une solution particulière de 
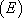, elle vérifie donc 
.
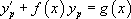Par ailleurs,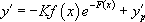 
, donc :
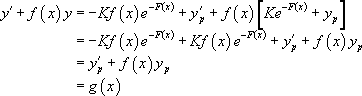
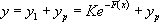est bien solution de 
.
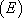Cette méthode repose entièrement sur la connaissance de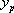 
qui n’est pas toujours facile à obtenir. La méthode de variation de la constante (§3.2.1) est par contre beaucoup plus générale.
Exemple :
« Résoudre l’équation  |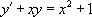
On utilise cette technique lorsqu’on ne peut pas trouver de solution particulière de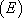 
. On résout dans ce cas l’équation SSM qui fournit 
.
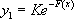On rappelle que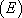 
s’écrit 
.
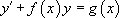On prend alors comme fonction inconnue 
, ce qui revient à faire de K, qui était constante pour l’équation SSM, une fonction inconnue de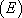 
.
Autrement dit, on fait varier la constante.
En posant dans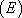 
, 
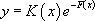, on obtient :
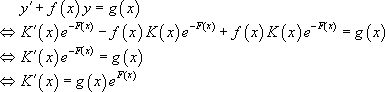
Ainsi, par intégration et sous réserve que l’on puisse calculer une primitive de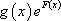 
, on obtient :
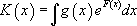
Finalement, la solution générale de l’équation différentielle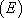 
s ‘écrit :
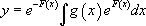
Exemples :
« Résoudre l’équation  |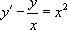
|
« Résoudre l’équation  |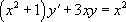
Nous considérons cette fois-ci des équations différentielles linéaires du premier ordre à coefficients constants, c’est-à-dire de la forme :
: 
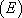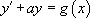avec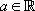 
une constante.
Ce cas est un cas particulier des équations différentielle du premier ordre que nous avons vu au paragraphe 3.2. En effet, nous avons ici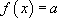 
.
Ainsi, après avoir résolu l’équation SSM, la méthode précédente s’applique, soit avec recherche d’une solution particulière, soit par variation de la constante.
Cependant, avec les équations différentielles linéaires du premier ordre à coefficients constants, la solution particulière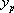 
s’obtient parfois simplement :
- Si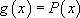 
un polynôme de degré n, alors 
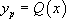un polynôme de degré n ;
- Si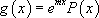 
, alors on pose 
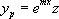, et z devient la fonction inconnue de l’équation différentielle 
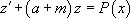: on est ramené au cas précédent.
Exemples :
« Résoudre l’équation  |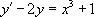
|
« Résoudre l’équation  |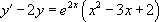
