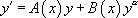Equations Différentielles

4         Compléments sur les équations différentielles du premier ordre

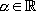Nous allons voir dans ce paragraphe quatre types d’équations différentielles du premier ordre, pour lesquelles il existe des méthodes permettant de les simplifier

4.1         Equation de Bernoulli

Une équation de Bernoulli est de la forme 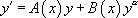 avec .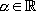

Lorsque 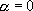 ou que 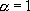, une telle équation est linéaire.

Pour 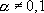, on peut s’arranger pour qu’elle le devienne ; on écrit :

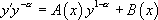
Or, on peut remarquer que 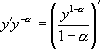. Donc en posant 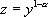, il vient :

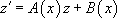
On est donc ramené à une équation linéaire que l’on sait résoudre.

Exemple :

«     Résoudre l’équation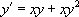

Réponse

4.2       Equation de Riccati

Une équation de Riccati est de la forme .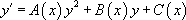

On ne peut la résoudre que si l’on connaît a priori une solution particulière .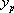

On pose alors 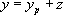, ce qui permet d’arriver à :

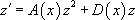
Il s’agit d’une équation de Bernoulli (voir ci-dessus).