Chapitre Complémentaire 1 : Nombres complexes
3
Nombres réels, nombres imaginaires purs. Notations algébrique
et trigonométrique des nombres complexes
Les nombres de la forme 
ont leur image située sur l’axe des x. Nous pouvons confondre l’ensemble des
réels et l’ensemble des nombres complexes du type .
Les nombres z de
la forme ont leur image située sur l’axe des y. On dit qu’ils sont imaginaires purs. L’argument d’un
nombre imaginaire pur est à près.
Exemple :
Le nombre est situé sur l’axe des x ; il est réel.
Le nombre est un nombre imaginaire pur.
3.1
Le nombre i
Le nombre imaginaire pur de module 1 et d’argument (à près) est désigné par i.
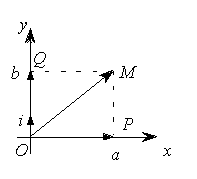
Figure 5
Le nombre complexe d’image M
est la somme des nombres et ayant pour images respectives P et Q :
Or et d’après les définitions précédentes :
est la forme
algébrique de z .
a est la partie réelle de z : .
b est la partie imaginaire de z : .
Exemple :
D’autre part, et .
On peut alors écrire :
qui est la forme
trigonométrique de z.
Exemple :
Le nombre i ayant
pour module 1 et pour argument ,
le nombre a pour module 1 et pour argument ,
ce qui conduit à :
3.2
Propriétés supplémentaires