N’hésitez pas à consulter la liste des symboles en cas de doute sur leur signification
Fonctions – Généralités
1 Définitions
1.1 Intervalles – voisinage
a et b étant deux réels, l’ensemble est l’intervalle ouvert noté ;
a et b sont les bornes de l’intervalle.
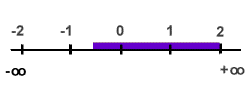
L’ensemble est l’intervalle fermé noté , bornes comprises.
Les intervalles ( ) et ( ) sont semi-ouverts (ou semi-fermés).
Par extension, on a :
ceci qui s’écrit aussi
L’intervalle est exactement égal à . On note .
Dans ce cours, on appellera voisinage de a, , tout intervalle ouvert de contenant a. Ainsi, , est un voisinage de a.

1.2 Fonctions réelles d’une variable réelle
Une fonction (ou application) réelle d’une variable réelle est une transformation qui à tout élément d’une partie (souvent appelée domaine) fait correspondre un unique élément de . Ainsi :
|
, tel que |
|
Par exemple, la température d'une espèce de lézard (y) en fonction de la température de l'air à l'ombre (x) est approximativement :
La température (y) d’une souris dans les mêmes conditions sera approximativement : avec c constante |
D (souvent noté ) est l’ensemble de définition (ou ensemble de départ) de f. D est le plus souvent un intervalle ou une réunion d’intervalles.
est l’ensemble d’arrivée de f ou image de D par f :
et
Remarque :
Les éléments de sont appelés les images.
Les éléments de D sont appelés les antécédents.
Exemples :
(1) telle que Réponse
(2) telle que Réponse
(3) telle que Réponse
1.3 Graphe d’une fonction
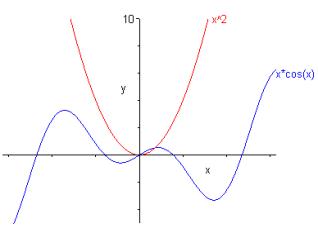
Le graphe d’une fonction f (ou courbe représentative de f) dans un repère cartésien , en général orthonormé, est l’ensemble des points de coordonnées , avec domaine de définition de f : .
Exemple :