Fonctions – Généralités

3         Fonction composée – Fonction réciproque

3.1         Fonction composée

Définition :

Soient deux fonctions, f définie sur un intervalle  et g définie sur un intervalle  tel que  (i.e.,  ).

La fonction composée  est la fonction définie sur I par  :

                       

où  et , afin que  existe.

 

Remarque : Si  existe, la fonction composée  n’existe pas toujours, et lorsque  existe alors en général .

 

Exemples :

· Soient           f définie par  avec

g définie par  avec

Que peut-on dire de  et  ?                                       Réponse

· Soient           f définie par  avec

g définie par  avec .

Que peut-on dire de  et  ?                                       Réponse

3.2       Injectivité, surjectivité, bijectivité

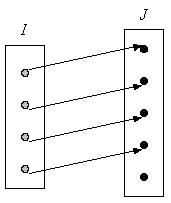
·        On dit qu’une fonction  est injective si tout élément de  est l’image d’un seul élément de I. Autrement dit, f est injective si et seulement si :

L’injectivité d’une fonction se traduit également par le fait que « tout élément de J admet au plus un antécédent par f dans I ».

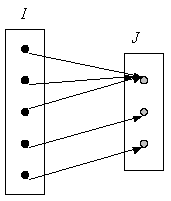
·        On dit qu’une fonction  est surjective si , autrement dit si tout élément de J est l’image par f d’au moins un élément de I.

 

 

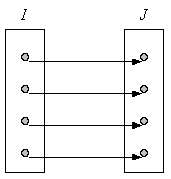
Remarque : La fonction  est toujours surjective.

·        On dit qu’une fonction  est bijective si elle est à la fois injective et surjective.

 

Exemples :

(1) Considérons la fonction définie sur  par .

f est-elle surjective ? injective ?                                                                       Réponse

 

(2) Considérons maintenant la fonction définie par , avec .

f est-elle surjective ? injective ?                                                                       Réponse

3.3       Fonction réciproque

3.3.1                   Définition

Définition :

Soit . On dit que f admet une fonction réciproque s’il existe  telle que  et .

On dit alors que g est la fonction réciproque de f et on note .

 

Proposition :

Soit . Alors f admet une fonction réciproque si et seulement si f est bijective.

 

Démonstration

 

Remarques :

(i)                  Par extension, la définition et la proposition précédentes restent valables pour une fonction , où  et  sont des parties de .

(ii)                Sous l’hypothèse que  existe, si l’image de x par f est y, alors l’image de y par  est x ; en d’autres termes :

   

(iii)               Il ne faut pas confondre la fonction réciproque , avec la fonction inverse .

3.3.2                 Conséquences

Si  existe, alors , où  est la fonction identité :

 donc  avec

 donc  avec

Du point de vue graphique, les représentations de deux fonctions réciproques se déduisent l’un de l’autre par une symétrie par rapport à la première bissectrice.

 

Justification

 

Exemples :

· Soit la fonction f définie par  avec .

On a donc  d’où l’on tire .

Donc la fonction réciproque de f est définie par .                         Vérification

· Soit la fonction f définie par .

La fonction réciproque g est alors définie par .                          Vérification

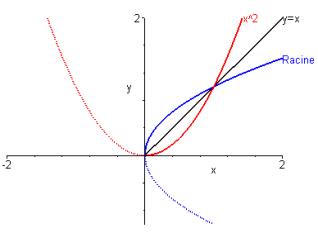
3.3.3                 Application : définition de la fonction racine carrée

Soit la fonction f définie sur  par :

Nous avons vu plus haut que la fonction f n’est pas bijective puisqu’à une valeur de y correspondent deux valeurs de x ; par conséquent elle n’admet pas de fonction réciproque.

Par contre, si on réduit l’ensemble de définition soit à  (  ) soit à  (  ), la même fonction f devient bijective, et admet alors une fonction réciproque.

Par convention, on choisit , et on appelle racine carrée de x, notée  cette fonction réciproque. D’où :

 

Une méthode fort ancienne (que l’on doit à Héron d’Alexandrie) permet d'extraire la racine carrée d'un nombre quelconque par un procédé itératif, autrement dit « comment calcule-t-on rapidement une racine carrée lorsque les batteries de la calculette sont épuisées? ».