Limites – Continuité

1.1.2 Limites en et

Définition (limite en ) :

Soit . On suppose que .

· Soit . On dit que est limite de f en si :

tel que

On note ou ou

· On dit que est limite de f en si :

tel que

· On dit que est limite de f en si :

tel que

Définition (limite en ) :

Soit . On suppose que .

· Soit . On dit que est limite de f en si :

tel que

On note ou ou

· On dit que est limite de f en si :

tel que

· On dit que est limite de f en si :

tel que

Proposition :

Si , alors

1.1.3 Limite par valeurs supérieures ou inférieures

Définition :

Soit telle que ( ). Quand x tend vers , on dit que tend vers par valeurs supérieures (resp. inférieures) si, au voisinage de , (resp. ).

On note alors (resp. ).

Exemple

Considérons la fonction définie par . On a et .

Graphe

1.1.4 Limites à gauche et à droite

Définition (limite à gauche) :

Soit . Alors

tel que .

Définition (limite à droite) :

Soit . Alors

tel que .

1.2 Limites par opération

1.2.1 Limite d’une somme



						?

? on parle alors de forme indéterminée

1.2.2 Limite d’un produit

	0	ou
ou	ou	ou
ou	?	ou

ou : on décide de suivant le signe de , en appliquant la règle des signes.

1.2.3 Limite d’un quotient

		ou	0	ou
0	ou		0	ou
ou	0	ou	?	?

ou : on décide de suivant le signe de , en appliquant la règle des signes.

Remarques :

· Lorsque le numérateur tend vers zéro et le dénominateur vers l’infini, le quotient tend vers zéro : ou selon la règle des signes.

· Lorsque le numérateur tend vers l’infini et le dénominateur vers zéro, le quotient tend vers l’infini : ou selon la règle des signes.

1.3 Limites par comparaison

Soit .

Proposition 1 :

S’il existe une fonction g et un réel A tels que et , alors : .

Proposition 2 :

S’il existe une fonction g et un réel A tels que et , alors : .

Théorème « des gendarmes » :

S’il existe deux fonctions g et h, un réel A tels que et et , alors .

Proposition 3 :

S’il existe une fonction g et un réel A tels que et , alors : .

Proposition 4 :

S’il existe deux fonctions f et g et un réel A tels que ; si et , alors .

1.4 Limite d’une fonction composée

Théorème :

Soient , et des nombres réels (« éventuellement » égaux à ).

Soient f et g deux fonctions dont la composée existe.

Si et si , alors .

1.5 Limite à l’infini d’une fonction polynôme ou d’une fraction rationnelle

Méthode :

Pour déterminer une limite à l’infini d’une fonction polynôme ou rationnelle, dans le cas où les théorèmes précédents ne s’appliquent pas, on transforme l’expression en factorisant chaque polynôme par le terme de plus haut degré.

? Cas d’une fonction polynôme

On cherche à calculer avec .

On a et ; la somme est indéterminée.

On transforme le polynôme : .

Or et ;

Donc comme somme et comme produit .

a La limite à l’infini d’un polynôme est la limite de son terme de plus haut degré

? Cas d’une fraction rationnelle

On cherche à calculer avec .

et ; le quotient est donc indéterminé.

Pour , on a : . Ainsi :

et , donc : et . Finalement :

et donc

a La limite à l’infini d’une fraction rationnelle est égale à la limite du quotient simplifié de ses termes de plus haut degré

1.6 Limites et courbe représentative d’une fonction

1.6.1 Etude des branches infinies

Considérons une fonction f définie sur un domaine de . Soit sa courbe représentative.

Proposition 1 :

Si , alors la droite est asymptote à la courbe .

Proposition 2 :

Si , alors la droite est asymptote à la courbe .

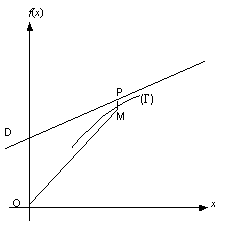
1.6.2 Direction asymptotique

On recherche une direction asymptotique lorsque .

D’après AZOULAY et AVIGNANT

La courbe admet une direction asymptotique si la droite OM tend vers une position limite lorsque le point M s’éloigne à l’infini sur .

Le coefficient directeur de OM est . S’il existe une direction asymptotique, alors tend vers une limite finie .

Si lorsque , on dit que admet une branche parabolique dans la direction Oy.

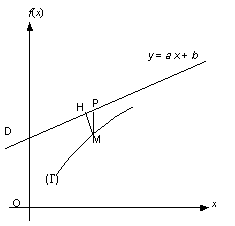
1.6.3 Asymptotes

D’après AZOULAY et AVIGNANT

La courbe admet une asymptote oblique D d’équation , si la distance entre M et la droite D ( ) tend vers 0 lorsque M s’éloigne à l’infini sur .

La pente de D est :

Pour déterminer l’ordonnée à l’origine de D, on montre que tend vers b lorsque , ou bien alors que tend vers 0 lorsque .

Si , on dit que admet une branche parabolique de pente a.