On rappelle que dans ce chapitre I est un intervalle ouvert de .
Définitions :
Soit dérivable en . Alors f admet un développement limité d’ordre 1 en :
avec et
1. est l’approximation polynomiale de degré 1 de f en .
2. L’équation est l’équation de la tangente désignée par T à la courbe représentative de f, au point .
Le nombre dérivé est le coefficient directeur (ou pente) de la tangente.
Propriétés :
Soit dérivable en . Soit courbe représentative de f.
est donc la pente de la tangente T à au point .
(i) Si , alors T est une droite parallèle à l’axe des x ;
(ii) Si , alors T est une droite parallèle à l’axe des y.
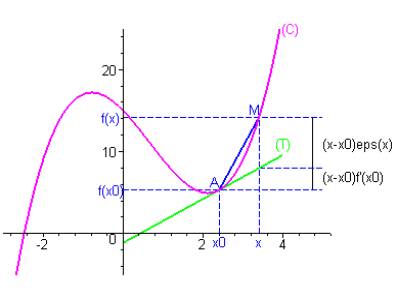
Soit et sur la courbe représentative (C) de la fonction f.
Le taux d’accroissement correspond au coefficient directeur de la corde AM.
Dire que f est dérivable en revient à dire que la corde AM possède une position limite non verticale (T) de coefficient directeur quand x tend vers , c’est-à-dire quand M tend vers A.
(T) est la tangente à (C) au point d’abscisse .

Ce qui précède est inspiré du chapitre 8 « Dérivation, connexité », une aide à l’interprétation géométrique de la notion de dérivée et de tangente à une courbe sur le site M@ths En Prép@.