Fonctions usuelles

3         Fonctions logarithme et exponentielle

3.1                       Introduction

C’est dans le but de simplifier les calculs trigonométriques de l'astronomie que Neper invente les logarithmes (le terme est de lui, du grec logos = logique, raison et arithmos = nombre).

Il en expose le fonctionnement dans deux traités : Mirifici Logarithmorum Canonis Descriptio (1614), puis Mirifici Logarithmorum Canonis Constructio (posthume, 1619) soit : « Description (resp. Construction) de la Règle Admirable des Logarithmes ».

3.2                       La fonction logarithme népérien

Comme la fonction  est dérivable sur , elle admet une primitive sur cet intervalle (donc une infinité) ; en particulier on peut trouver une primitive qui s’annule en .

 

·        La fonction logarithme népérien est donc définie sur  par .

·       

·        Pour tout , l’aire du domaine délimité par l’axe des abscisses, la courbe  et les droites d’équation  et  correspond exactement au calcul suivant :

 si

 si                                                            Voir

Propriétés : Pour tout  et pour tout , alors :
(i)	(ii)
(iii)	(iv)

Démonstration

·        La fonction ln est dérivable sur  : ,

·        La fonction ln est strictement croissante sur

·                                                      (par définition de la dérivée)

 

 

Remarque

 

Aller vers… : Le point de vue géométrique de X. Hubaut est une autre façon de retenir la définition de la fonction logarithme népérien.

 

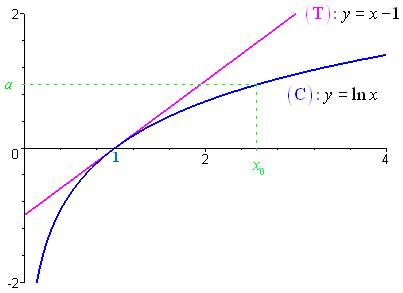
La fonction  :

3.3                       La fonction exponentielle

 

Par conséquent, , l’équation  admet une unique solution  (voir figure ci-dessus).

 

Conséquence :

L’équation  admet une unique solution . En effet : .

 

 

·        La fonction exponentielle est définie sur .

·        ,

·         et  :

      

Propriétés : Pour tout  et pour tout , alors :
(i)	(ii)
(iii)	(iv)

 

Exemple :

·        La fonction exponentielle est dérivable sur  :

·        La fonction exponentielle est strictement croissante de  sur

·                                                         

 

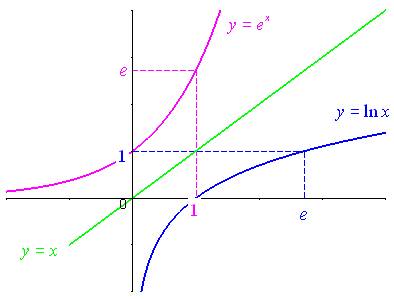
La fonction  : .

3.4                       Exemples d’utilisation en Biologie

3.4.1                   La fonction exponentielle

L’exemple qui suit est extrait de Lomen et Lovelock, 1999, p51.

 

Pendant la première moitié du 20^ème siècle, les populations de tourterelles turques (« collared dove ») envahissent l’Europe d’Est en Ouest. Cet oiseau était très rare en Grande-Bretagne avant1955. L’invasion de cette espèce en Grande-Bretagne est d’un intérêt tout particulier pour les ornithologues ce qui les a conduit à faire des recensements de populations réguliers entre 1955 et 1964.

On peut raisonnablement supposer que le nombre de tourterelles turques est proportionnel au nombre d’endroit où l’espèce est recensée. Ainsi, les relevés ornithologiques de l’époque fournissent les données suivantes :

 

 

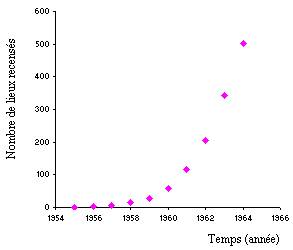
On constate que l’augmentation du nombre de lieux où la tourterelle turque a été recensée augmente de façon exponentielle sur les 10 années de mesure. Ainsi, on peut considérer que :

Si t désigne l’année et N le nombre de lieux où la tourterelle turque a été recensée. Les paramètres  sont choisis pour décrire « au mieux » la série de données.

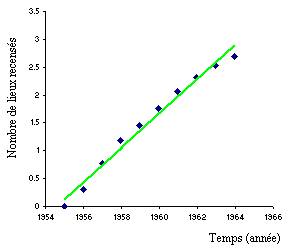
Une transformation logarithmique permet d’écrire :

Ainsi, la représentation de  en fonction de t est une droite, ce que permet de vérifier le graphe ci-dessous :

3.4.2                 La fonction logistique

L’exemple qui suit est extrait de Lomen et Lovelock, 1999, p42.

 

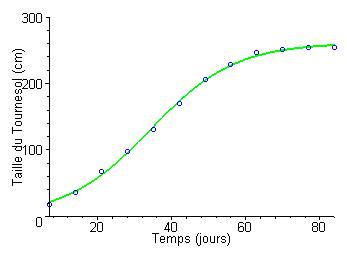
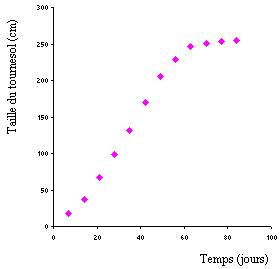
Dans le tableau ci-dessous, on peut voir l’évolution dans le temps de la taille moyenne d’un plan de tournesol :

 

 

On constate que pour de faibles valeurs du temps, la taille augmente de façon linéaire, puis que pour des temps plus important la croissance ralentit.

La fonction logistique est la plus classique pour décrire ce genre de données expérimentales.

Si on désigne par T la taille du plan de tournesol et par t le temps, on peut alors écrire :

En choisissant au mieux les valeurs des paramètres , on peut construire la courbe qui « passe au mieux » entre les points expérimentaux :