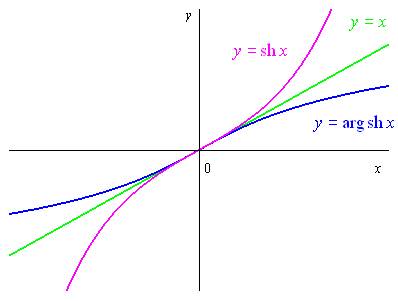Par définition, on appelle cosinus hyperbolique de x,
la quantité notée :
De la même manière, on définit le sinus hyperbolique,
notée :
On constate que et que .
Il vient alors immédiatement :
Par analogie avec les fonctions trigonométriques, on définit
la tangente hyperbolique, notée
(ou bien
) par :
On utilise quelquefois la co-tangente hyperbolique, notée
,
et définie par :
Les deux relations suivantes découlent immédiatement
de la relation (1) :
4.2.1
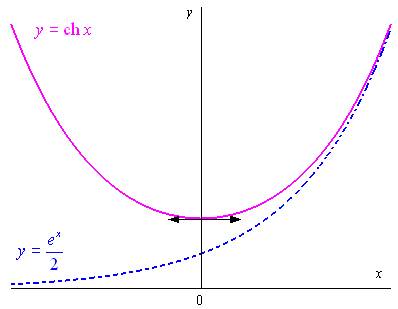
Etude de la fonction
La fonction paire : on fait l’étude sur
et le graphe est symétrique par rapport à
.
:
la fonction est strictement croissante sur
4.2.2
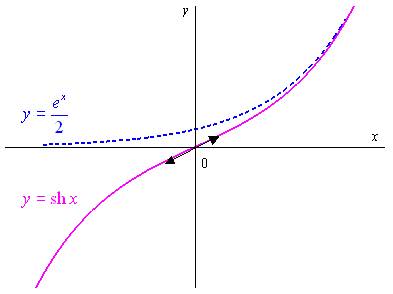
Etude de la fonction
La fonction impaire : on fait l’étude sur
et le graphe est symétrique par rapport à
l’origine.
:
la fonction est strictement croissante sur
Remarque :
entraîne que
.
4.2.3
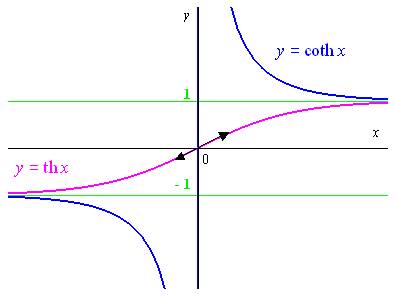
Etude de la fonction
La fonction impaire : on fait l’étude sur
et le graphe est symétrique par rapport à
l’origine.
La droite
est asymptote en
:
la fonction est strictement croissante sur
Dans la rubrique aides-mémoire, vous trouverez un formulaire récapitulatif des formules
usuelles impliquant les fonctions hyperboliques.
4.4.1
Définition de la fonction réciproque du cosinus hyperbolique
Définition :
La fonction réciproque du cosinus hyperbolique se note
et se définit par :
est une fonction continue, croissante et
bijective de
sur
.
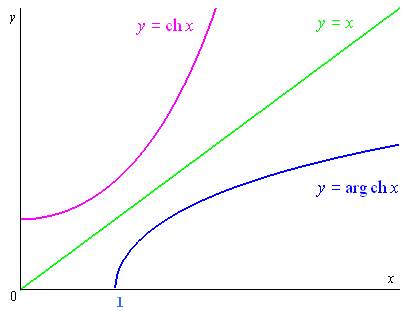
Expression logarithmique de
De la définition précédente, il vient
.
Si on pose
,
alors
,
ce qui conduit par résolution de cette équation du second degré à
.
Ainsi :
4.4.2
Définition de la fonction réciproque du sinus hyperbolique
Définition :
La fonction réciproque du sinus hyperbolique se note
et se définit par :
pour tout
est une fonction continue, croissante et
bijective de
sur
.
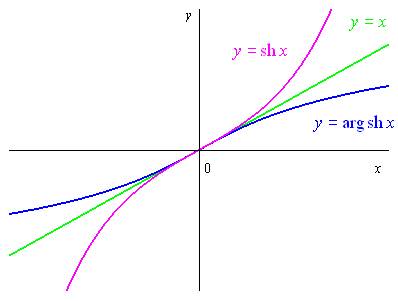
Expression logarithmique de
De la définition précédente, il vient
.
Si on pose
,
alors
,
ce qui conduit par résolution de cette équation du second degré à
.
Ainsi :
4.4.3
Définition de la fonction réciproque de la tangente
hyperbolique
Définition :
La fonction réciproque du tangente hyperbolique se note
et se définit par :
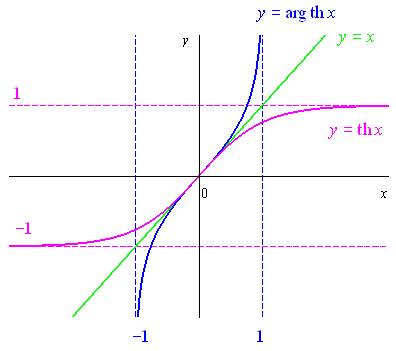
Expression logarithmique de
Par une démarche analogue aux précédente, on obtient :