Interprétation graphique :
Dans le cas d’une fonction
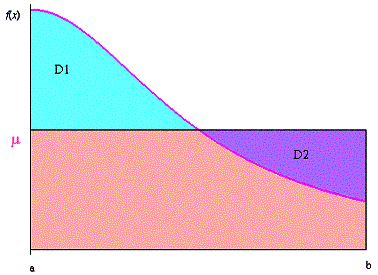
positive, la valeur moyenne d’une fonction est le réel µ tel que l’aire du rectangle de hauteur µ et de base (b-a) (rose + violet)
soit égal à l’aire sous la courbe (rose
+ bleu).
Les aires des domaines D1 (bleu) et D2 (violet)
sont identiques.
Exemple 13
Démonstration
Interprétation graphique :
Voir figure ci-dessous
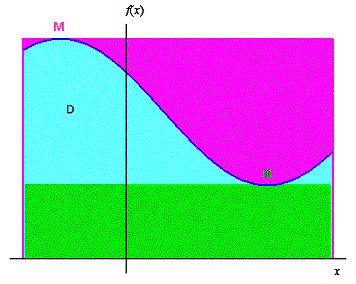
Dans le cas d’une fonction positive sur
et
,
l’inégalité de la moyenne (i) traduit le fait que l’aire du domaine D ( + ) comprise entre l’aire du rectangle de hauteur m et de base (b – a) ( ), et l’aire du rectangle de hauteur M et de même base ( ).