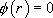|
Equation différentielle du premier ordre linéaire à coefficients constants :
|
Solution particulière Soit |
| Second membre de la forme :
|
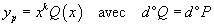
|
| Second membre de la forme :
|
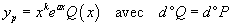
|
| Second membre de la forme :
|
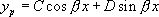 |
|
Equation différentielle du second ordre linéaire à coefficients constants :
|
Solution particulière Soit |
| Second membre de la forme :
|
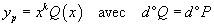
|
| Second membre de la forme :
|
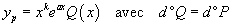
|
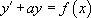
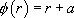 l’équation caractéristique
l’équation caractéristique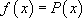 avec
avec 
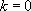 si 0 n’est pas solution de l’équation
si 0 n’est pas solution de l’équation 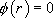
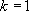 si 0 est solution de l’équation
si 0 est solution de l’équation 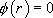
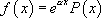 avec
avec 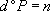
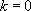 si
si 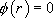
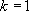 si
si 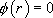
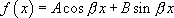
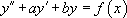
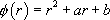 l’équation caractéristique
l’équation caractéristique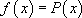 avec
avec 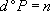
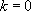 si 0 n’est pas solution de l’équation
si 0 n’est pas solution de l’équation 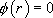
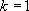 si 0 est une racine de l’équation
si 0 est une racine de l’équation 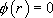
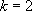 si 0 est racine double de l’équation
si 0 est racine double de l’équation 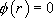
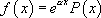 avec
avec 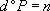
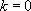 si
si 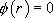
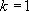 si
si 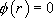
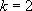 si
si