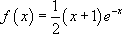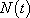la taille de la population l’année t, exprimée en milliers d’habitants.Il est possible de décrire au moyen d’une équation différentielle l’évolution de la taille de la population d'un pays qui présente les caractéristiques suivantes : par an, le taux de renouvellement est de 20 pour 1000 habitants, et le taux de mortalité est de 15 pour 1000 habitants.
Soit 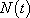la taille de la population l’année t, exprimée en milliers d’habitants.
La variation annuelle de la taille de la population peut être quantifiée à l’aide de la quantité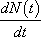 
. Ainsi, on peut écrire, par le jeu d’une balance entre renouvellement naturel et mortalité :
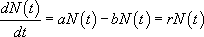
avec :
- a le taux de renouvellement de la population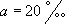 
;
- b le taux de mortalité de la population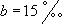 
;
- r le taux d’accroissement absolu de la population :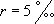 
.
Pour connaître l’évolution de N en fonction de t, il faut maintenant résoudre :
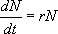
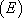
Il s’agit d’une équation différentielle à variable séparable qui s’intègre simplement :
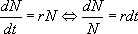
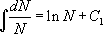
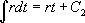
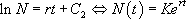
La valeur de K dépend de la condition initiale choisie. Si on suppose que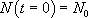 
, il vient :
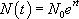
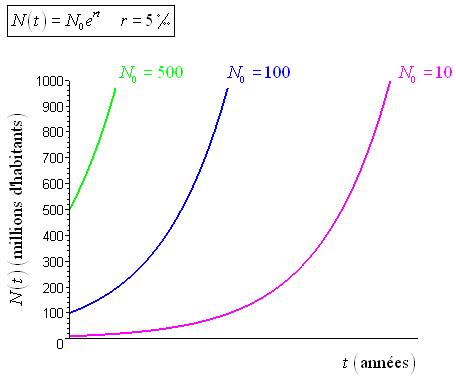
Voici la représentation graphique de la relation N en fonction de t pour différentes valeurs de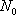 
:
Pendant une période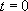 
à 
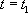du développement d’un organisme, on admet que la vitesse de croissance pondérale est proportionnelle à son poids. On obtient alors ‘équation suivante :
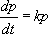avec p le poids (en g) et k le taux d’accroissement (I)
Le temps est exprimé en jours.
On sait d’autre part qu’à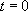 
, 
.
Cette équation à variables séparables s’intègre facilement (voir ci-dessus) :
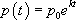
A l’aide de mesure faites sur un grand nombre d’individus, on a obtenu les résultats suivants :
A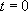 
, 
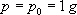
A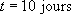 
, 
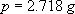
Ces données expérimentales permettent d’estimer une valeur pour k :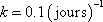 
.
On peut ainsi tracer grossièrement l’évolution du poids de l’organisme au cours de la croissance (courbe rose) :
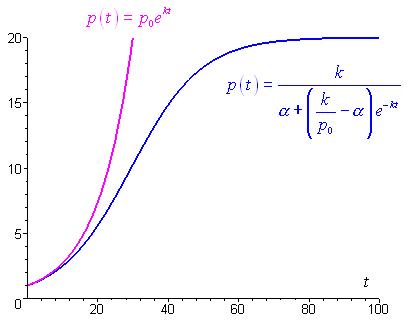
Cependant, il paraît peu probable que la croissance pondérale de l’organisme considère soit aussi rapide, et surtout illimitée. On est alors amené à proposer une autre équation, qui fait intervenir un terme de ralentissement de la croissance :
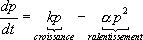(II)
Cette équation est aussi à variables séparables :
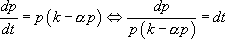
Pour intégrer l’équation, il faut alors faire une décomposition en éléments simples :
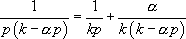
Ainsi :
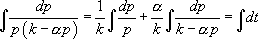
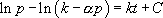
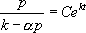
On obtient finalement :
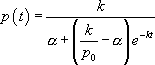
Une rapide étude de cette fonction permet de voir que :
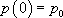(ce que l’on attendait) et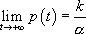 
Enfin, par un raisonnement simple, on montre que pour des temps petits (proches de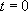 
), on a 
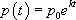. Ceci signifie que les courbes intégrales des équations (I) et (II) sont confondues pour des valeurs de t faibles (voir courbe bleue).
On désigne par f la densité de probabilité de rencontre entre deux animaux dans des conditions déterminées (par exemple en laboratoire). On suppose que cette densité de probabilité est fonction du temps :
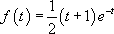
Une rapide étude de fonction conduit à la représentation graphique suivante :
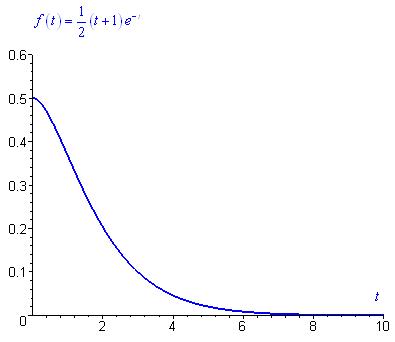
On peut alors calculer la probabilité p que deux animaux se rencontrent entre les instants 
et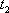 
à l’aide de l’intégrale suivante :
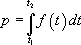
Ainsi,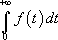 
est nécessairement égale à 1 (probabilité que deux animaux se rencontrent entre 
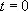et l’infini) :
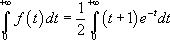
Ce calcul s’effectue à l’aide d’une intégration par partie :
On pose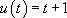 
et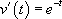 
. Il vient 
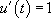et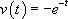 
.
Ainsi,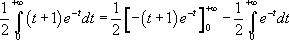 
. En tenant compte du fait que 
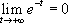, on obtient :*
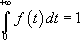
Pour revenir aux équations différentielles, on peut chercher à résoudre l’équation suivante :
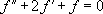
L’équation caractéristique est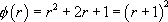 
, ce qui conduit immédiatement à la solution générale :
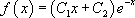
Si on cherche la solution particulière telle que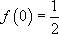 
et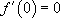 
, on retrouve exactement :
