Chapitre 2 : Probabilités
2 Espace fondamental et évènements
La théorie des ensembles qui est succinctement présentée
dans ce chapitre constitue un outil puissant dans plusieurs branches des
mathématiques, notamment en probabilités.
2.1
Définitions
En face de situations dont l’issue est incertaine, on a bien souvent envie d’attribuer à chacune des
éventualités possibles une vraisemblance plus ou moins grande. Afin de donner
une rigueur mathématique à ce concept, il est nécessaire tout d’abord de donner
quelques définitions.
• Une expérience ou une épreuve
est qualifiée d’aléatoire
si on ne peut pas prévoir son résultat et si, répétée dans des conditions
identiques, elle peut donner des résultats différents.
• Le résultat d’une expérience noté w constitue une éventualité ou un événement élémentaire.
• l’ensemble des évènements élémentaires possibles pour une expérience aléatoire donnée constitue l’espace fondamental appelé univers ou univers des possibles noté W.
Exemple :
Lors d’un contrôle sanguin, l’ensemble des résultats
possibles si l’on s’intéresse
(1) au groupe sanguin et au
facteur rhésus d’un individu est
W = íA+,A-,B+,B-,AB+,AB-,O+,O-ý
(2) au nombre de globules
blancs W = N*= í1,2,…..n,…… ý
(3) au
taux de glycémie W = [0 ;15] au-delà de
15, l’individu n’est plus en état de subir une prise de sang.
Ainsi pour une même
épreuve, l’univers W
peut être fini
(toutes les éventualités sont connues : cas 1) ou infini (toutes les éventualités ne
sont pas connues : cas 2 et 3). Dans ces deux derniers cas, l’univers peut
être dénombrable
si on peut numéroter les éventualités connues (cas 2) ou bien continu
comme dans le cas du taux de glycémie (cas 3).
Un
évènement
quelconque A est un ensemble
d’évènements élémentaires et constitue une partie de l’univers des possibles W dont
on sait dire à l’issue de l’épreuve s’il est réalisé ou non.
Si w Î
A, alors A
est réalisé. Mais si w
Ï
A alors A n’est pas réalisé et c’est
, l’évènement contraire
qui est réalisé. Un évènement est donc une assertion relative aux résultats
d’une expérience.
Il est possible qu’un évènement ne soit constitué que d’un seul évènement
élémentaire.
Les évènements sont représentés par des lettres majuscules, A, B, C, A1, A2,
etc.
Exemple :
Dans l’exemple concernant les groupes sanguins,
- l’évènement A «
l’individu est de rhésus positif » est représenté par :
A = íA+,B+,AB+,O+ý avec
A Ì W
- l’évènement B
« l’individu est donneur universel » est représenté par :
B = {O-} un seul évènement élémentaire
Dans le cadre de cet exemple, l’évènement A est réalisé si le résultat du typage
donne l’un des 4 groupes sanguins A+,B+,AB+,O+.
| Remarque : |
Pour ce même exemple, le résultat
« la glycémie vaut
»
ne constitue
pas un évènement car il est impossible de savoir s’il est réalisé ou non. |
|
Toute partie de W n’est pas forcément un évènement. Ainsi il faut toujours définir après avoir déterminé l’univers W, l’ensemble des évènements e(W).
|
Si W est fini, chaque partie A de l’univers W (A Ì W) est
constituée d’un nombre fini d’éventualités et dans ce cas l’ensemble des évènements est tel que :
e(W) = P (W) l’univers des possibles
Dans le cadre de ce cours, nous nous placerons dans le cas
où l’ensemble des évènements de
l’univers W
est clairement défini.
2.2
Evènements remarquables
L’évènement
impossible
noté ø est l’évènement qui ne peut être réalisé quelle que
soit l’issue de l’épreuve. Bien que constitué d’aucune éventualité, ø est considéré comme un évènement :
L’évènement certain, noté W
est toujours
réalisé quelle que soit l’issue de l’épreuve. Il est constitué de
toutes les éventualités et l’on impose que ce soit un évènement :
L’évènement contraire ou complémentaire d’un évènement A, noté CA ou
est l’évènement qui est réalisé si et
seulement si A ne l’est pas.
Il est donc constitué des évènements élémentaires w qui ne sont pas dans
A.
Le complémentaire CA ou
correspond à la négation logique non -A.
Exemple :
Dans l’exemple
concernant les groupes sanguins, l’évènement contraire de A « l’individu est de rhésus positif » est constitué des
évènements élémentaires suivant :
= íA-,B-,AB-,O-ý
Par définition, on obtient les relations suivantes :

2.3
Opérations sur les évènements
Si l’on considère simultanément la réalisation de deux
évènements A et B, il est possible d’effectuer des opérations sur ces ensembles.
2.3.1
L’intersection de deux évènements
On appelle intersection de deux évènements A et B,
l’évènement qui est réalisé si et seulement si A et B le sont. Il est donc constitué des éventualités appartenant à la
fois à A
et B.
C’est un évènement noté A Ç B tel que : "A, B Î e(W), A Ç B Î e(W)
avec
L’intersection A Ç
B correspond à la conjonction
logique « A et B ».
 |
|
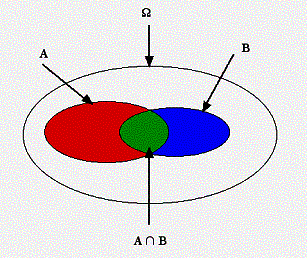
L’intersection
des deux évènements A et B figure en vert sur le graphe ci-contre.
|
| Remarque : |
L’univers des possibles W n’étant pas limité uniquement aux évènements A (parties rouge et verte) et B (parties bleu et verte), |
|
l’évènement complémentaire
, est formé des parties bleu et blanche. |
Exemple :
Dans l’exemple
concernant les groupes sanguins, si à l’évènement A « l’individu est de rhésus positif », on ajoute l’évènement B « l’individu possède l’allèle
B », l’intersection de ces deux évènements donne : A
Ç
B = íB+,AB+ý
Deux évènements A
et B sont incompatibles ou disjoints,
s’ils ne peuvent être réalisés simultanément.
On a alors : A Ç B = Æ
Quelques propriétés de l’intersection (Ç ) :
 A Ç
= Æ évènements incompatibles
A Ç
= Æ évènements incompatibles
W Ç A = A élément neutre (W)
Æ Ç A = Æ élément absorbant (Æ)
A Ç B = B Ç A commutativité
A Ç (B Ç C) = (A Ç B) Ç C associativité
A Ç (B È C) = (A Ç B) È (A Ç C) distributivité avec la réunion (È)
2.3.2 La réunion de deux évènements
On appelle réunion de deux évènements A et B, l’évènement qui est réalisé si et seulement si A ou B est réalisé. Il est donc constitué des éventualités appartenant à A ou B.
C’est un évènement noté A È B tel que : "A,B Î e(W), A È B Î e(W)
avec
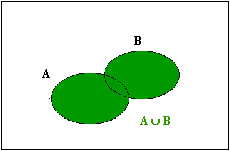
La réunion A È B correspond à la disjonction logique « A ou B ».
|
|
La réunion des deux évènements A et B figure en vert sur le graphe ci-contre.
|
| Remarque : |
La réunion de deux évènements n’est pas la somme algébrique des évènements dans la mesure où la zone de recouvrement n’est pas compatibilisée deux fois. |
|
|
Exemple :
Dans l’exemple concernant les groupes sanguins, si à l’évènement A « l’individu est de rhésus positif », on ajoute l’évènement B « l’individu possède l’allèle B », la réunion de ces deux évènements donne :
A È B = íA+,B+,B-,AB+,AB-,O+ý
Quelques propriétés de la réunion (È) :
 A È
= W évènements complémentaires
A È
= W évènements complémentaires
Æ È A = A élément neutre (Æ)
W È A = W élément absorbant (W)
A È B = B È A commutativité
A È (B È C) = (A È B) È C associativité
A È (B Ç C) = (A È B) Ç (A È C) distributivité avec l’intersection (Ç)
Selon les lois de Morgan, nous avons :
ce qui correspond à la partie hachurée sur ce graphe.
ce qui correspond à l’ensemble vide Æ lorsque l’univers des possibles W n’est constitué que des évènements A et B (graphe).
2.3.3 L’inclusion d’un évènement
Un évènement A entraîne un évènement B si la réalisation de A implique celle de B.
On dit que l’évènement A est inclus dans l’évènement B.
A Ì B
|
|
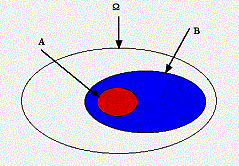
L’ implication logique " A fi B " se traduit par l’inclusion A Ì B .
Exemple de l’inclusion de l’évènement A en rouge dans l’évènement B en bleu.
|
Exemple :
Soit une urne contenant des billes rouges unies et des billes vertes unies et striées. Si l’on
note A l’événement « obtention d’une bille striée » et B l’événement « obtention d’une bille verte », la réalisation de A implique la réalisation de B car A est inclus dans B.
2.4 Système complet d’évènements
forment un système complet d’évènements si les parties
de W constituent une partition de W telle que :
Un système complet d’évènements est formé de toutes les parties de W, c’est-à-dire des familles d’évènements 2 à 2 incompatibles dont la réunion constitue l’évènement certain W.
Le nombre de partitions possibles dans un ensemble fini de n évènements est :
si Card (W) = n alors Card (P(W)) = 2n Illustration
2.5 Espace probabilisable
Supposons que l’ensemble des évènements constitue une classe C de P(W) , telle que :
C Í P(W)
On appelle espace probabilisable (W,C), un objet formé de deux éléments :
- un espace d’éventualités W
- un espace d’évènements C Í P(W)
avec :
(P1) A Î C Þ
Î C
(P2)
Î C ("i Î N*) Þ
Î C
(P3) W Î C
Ces trois axiomes ou propriétés suffisent à définir un espace probabilisable et on pourrait montrer qu’il implique que Æ Î C et
Î C
![]()