Exemple :
Afin d’étudier la structure de la population de gélinottes
huppées (Bonasa umbellus)
abattues par les chasseurs canadiens, une étude du dimorphisme sexuel de cette
espèce a été entreprise. Parmi les caractères mesurés figure la longueur de la
rectrice centrale (plume de la queue). Les résultats observés
exprimés en millimètres sur un échantillon de 50 mâles juvéniles sont notés
dans la série ci-dessus :
|

La gélinotte huppée
|
153
|
165
|
160
|
150
|
159
|
151
|
163
|
|
160
|
158
|
149
|
154
|
153
|
163
|
140
|
|
158
|
150
|
158
|
155
|
163
|
159
|
157
|
|
162
|
160
|
152
|
164
|
158
|
153
|
162
|
|
166
|
162
|
165
|
157
|
174
|
158
|
171
|
|
162
|
155
|
156
|
159
|
162
|
152
|
158
|
|
164
|
164
|
162
|
158
|
156
|
171
|
164
|
|
158
|
|
|
|
|
|
|
4.2
Tableaux statistiques
Le tableau de distribution de fréquences est un mode
synthétique de présentation des données. Sa constitution est immédiate dans le
cas d’un caractère discret mais nécessite en revanche une transformation des
données dans le cas d’un caractère continu.
4.2.1
Fréquences absolues, relatives et cumulées
A chaque modalité xi du caractère X, peut correspondre un ou plusieurs
individus dans l'échantillon de taille n.
| Remarque : |
On
peut noter que
,
taille de l’échantillon et
|
|
|
4.2.2 Caractères quantitatifs discrets
Dans le cas d’un caractère quantitatif discret, l’établissement
de la distribution des données observées associées avec leurs fréquences est
immédiate.
Exemple :
|

|
La cécidomyie du hêtre provoque sur les feuilles
de cet arbre des galles dont la distribution de fréquences observées est
la suivante :
|
|
Caractère X :
xi: nombre de galles
par feuille
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
ni : nombre de feuilles portant xi galles
|
182
|
98
|
46
|
28
|
12
|
5
|
2
|
1
|
0
|
1
|
0
|
|
fi : fréq. relative
|
0,485
|
0,261
|
0,123
|
0,075
|
0,032
|
0,013
|
0,005
|
0,003
|
0
|
0,003
|
0
|
|
fi cum. : fréq. relative
cumulée
|
0,485
|
0,746
|
0,869
|
0,944
|
0,976
|
0,989
|
0,994
|
0,997
|
0,997
|
1
|
1
|
La taille de l’échantillon étudié est n =375 feuilles
4.2.3
Caractères quantitatifs continus
Dans le cas d'un caractère quantitatif continu,
l’établissement du tableau de fréquences implique d’effectuer au préalable une répartition
en classes des données. Cela nécessite de définir le nombre de
classes attendu et donc l’amplitude associée à chaque classe ou intervalle de
classe.
En règle générale, on choisit des classes de même amplitude. Pour que la distribution en
fréquence est un sens, il faut que chaque classe comprenne un nombre suffisant
de valeurs (ni).
Diverses formules empiriques permettent d’établir le nombre de classes
pour un échantillon de taille n.
La règle de STURGE :
Nombre de classes = 1+ (3,3 log n)
La règle de YULE : Nombre de classes =
L'intervalle entre chaque classe est obtenu
ensuite de la manière suivante :
Intervalle de classe = (X max - X min) / Nombre de classes
avec X max et X min,
respectivement la plus grande et la plus petite valeur de X dans la série statistique.
A partir de Xmin
on obtient les limites de classes ou bornes de classes par addition successive de
l’intervalle de classe. En règle général, on tente de faire coïncider l’indice de
classe ou valeur centrale de la classe avec un nombre entier ou
ayant peu de décimales.
Exemple :
Dans le cadre de l’étude de la population de gélinottes huppées
(Bonasa umbellus),
les valeurs de la longueur de la rectrice principale peuvent être réparties de
la façon suivante :
• définition du
nombre de classes :
Règle de Sturge : 1 + (3,3 log 50) = 6,60
Règle de Yule :
= 6,64 les deux valeurs sont très peu différentes
• définition de
l’intervalle de classe :
IC =
= 5,15 mm que l’on arrondit à 5 mm par
commodité
• Tableau de
distribution des fréquences
|
Caractère X :
xi : longueur de la rectrice bornes des
classes
|
[140-145[
|
[145-150[
|
[150-155[
|
[155-160[
|
[160-165[
|
[165-170[
|
[170-175[
|
|
Valeur
médiane des classes, xi’
|
142,5
|
147,5
|
152,5
|
157,5
|
162,5
|
167 ,5
|
172,5
|
|
ni : nombre
d’individu par classe de taille xi
|
1
|
1
|
9
|
17
|
16
|
3
|
3
|
|
fi :
fréquence relative
|
0,02
|
0,02
|
0,18
|
0,34
|
0,32
|
0,06
|
0,06
|
|
fi cum. : fréquence relative
cumulée
|
0,02
|
0,04
|
0,22
|
0,56
|
0,88
|
0,94
|
1
|
4.3
Représentations graphiques
Les représentations graphiques ont l’avantage de renseigner
immédiatement sur l’allure générale de la distribution. Elles facilitent
l’interprétation des données recueillies.
4.3.1
Caractères quantitatifs discrets
Pour les caractères quantitatifs discrets, la représentation
graphique est le diagramme en bâtons où la hauteur des bâtons correspond à
l’effectif ni associé à
chaque modalité du caractère xi.
Exemple :
|
|
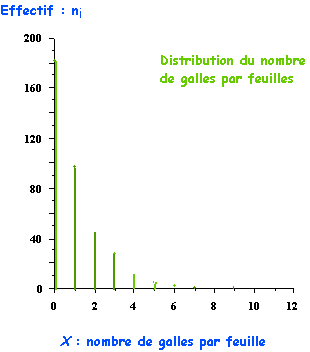
Dans l’exemple de la cécidomyie du hêtre, la
distribution des fréquences observées du nombre de galles par feuille peut
être représentée par un diagramme en bâtons
avec en ordonnée les effectifs ni et en abscisse les différentes modalités de la variable étudiée.
|
4.3.2
Caractères quantitatifs continus
Pour les caractères quantitatifs continus, la représentation
graphique est l’histogramme
où la hauteur du rectangle est proportionnelle à l’effectif ni. Ceci n’est vrai que si
l’intervalle de classe est constant. Dans ce cas l’aire comprise sous
l’histogramme s’avère proportionnelle à l’effectif total. En revanche lorsque
les intervalles de classe sont inégaux, des modifications s’imposent pour
conserver cette proportionnalité. Dans ce cas, en ordonnée, au lieu de porter
l’effectif, on indique le rapport de la fréquence sur l’intervalle de classe.
Ainsi la superficie de chaque rectangle représente alors l’effectif associé à
chaque classe.
Exemple :
|
|
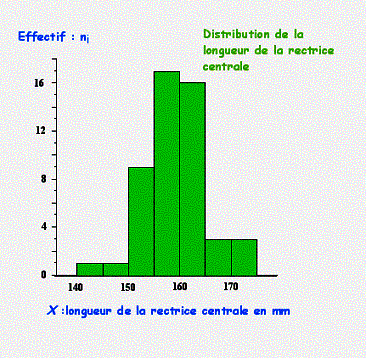
Dans l’exemple de la longueur de la rectrice centrale des
individus mâles de la gélinotte huppée, la distribution des fréquences
observées est représentée par un histogramme avec en
ordonnée les effectifs ni et en abscisse les limites de classe de la variable étudiée.
|



