Chapitre 9 : Analyse de Variance

3         Modèle de l’analyse de variance

3.1         Modèle sous H₀ : homogénéité des données

L’analyse de variance à un facteur teste l’effet d’un facteur contrôlé A ayant p modalités sur les moyennes d’une variable quantitative Y.

 

Les résidus e_ij correspondent aux fluctuations expérimentales pour chaque valeur de la variable y_ij mesurée.

Sous l’hypothèse    e_ij   ® N(0, s) ,   on montre que  y_ij   ® N(m, s)

              E(y_ij) = E(m+e_ij  ) = E(m) + E(e_ij ) = m + E(e_ij ) = m     puisque   E(e_ij ) = 0

              V(y_ij) = V(m+e_ij  ) = V(m) + V(e_ij ) = 0 + s²  = s²         puisque   V(e_ij ) = s²         

3.2       Modèle sous H₁ : hétérogénéité des données

 

Ainsi il existe une différence entre les moyennes de la variable selon les modalités du facteur controlé.

 

Remarque :	Tester l’hypothèse nulle «  absence d’effet sur facteur A » revient à tester
	H0 : les ai sont tous nuls

                             

3.3       Equation fondamentale de l’analyse de variance

3.3.1                   Estimation des paramètres des modèles

 

Sous H₀ : y_ij = m + e_ij    

             =          notée aussi y_..                         =  avec N =     

 L’ensemble des données du tableau peuvent être estimées à partir de la moyenne totale des y_ij   à laquelle s’ajoute la part d’aléatoire dans les mesures, e_ij .

 

Sous H₁ : y_ij = m + a_i + e_ij    

           notée aussi y_i.                         moyenne des y_ij pour la modalité i

d’où           

  et                       

ainsi      

 

 

 

 

3.3.2                 Décomposition de la variation totale

Soit le modèle sous H₁ :      y_ij = m + a_i + e_ij                                                            

 avec les estimateurs         

                                         

avec les écarts au carré                                             

avec les sommes pour tous les  individus j   

                                        

 or  = 0

car  = 0  sachant que E(e_ij) = 0 si les hypothèses initiales sont vérifiées.

avec la somme pour les p modalités du facteur controlé

                                     

 

Notation :

   SCE_totale = somme des écarts totaux ou variation totale = N

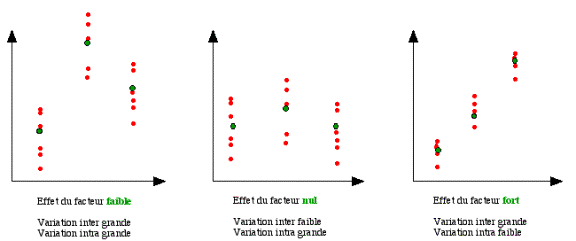
   SCE_inter = somme des écarts liés aux effets du facteur A ou variation inter (entre modalités)

   SCE_intra = somme des écarts résiduelles ou variation intra (interne à chaque modalité)

 

 

 

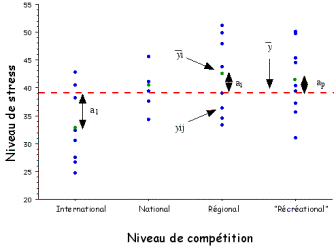
Exemple : Distribution des valeurs de la variable « anxiété des sportifs » yij en fonction des niveaux de compétition pour 30 sportifs.  : moyenne  pour chaque modalité i du facteur  en vert,  : moyenne de l’ensemble des données ai : effet de la modalité i sur la variable yij

 

3.3.3                 Le rapport de corrélation

 

C’est un indice de liaison, pas nécessairement linéaire entre les variables étudiées qui varie entre 0 et 1. Il mesure la qualité de l’ajustement des effets du facteur au travers des moyennes.