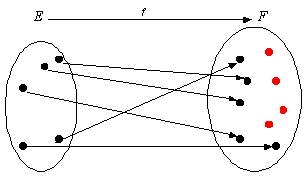
OUI !
· Il peut y avoir des éléments isolés dans F
NON !
· Deux éléments distincts de E ne peuvent pas avoir la même image dans F
Une application f : E ® F est dite injective si des éléments distincts de E ont des images distinctes : (contraposition).
|
|
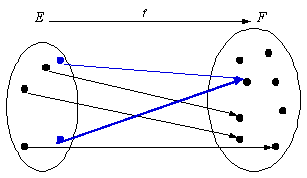
OUI ! · Il peut y avoir des éléments isolés dans F |
|
|
NON ! · Deux éléments distincts de E ne peuvent pas avoir la même image dans F |
Soit , f est injective si et seulement si .
Soit , f est surjective si tout vecteur de F possède au moins un antécédent par f dans E : .
|
|
OUI ! · Un élément de F peut avoir plusieurs antécédent dans E · Il peut y avoir des éléments isolés dans E |
|
|
NON ! · Il ne peut y avoir d'éléments isolés dans F |
f est surjective si et seulement si .
Soit , f est dite bijective si et seulement si elle est à la fois injective et surjective.
|
|
· Tout élément de E possède une image unique dans F · Tout élément de F possède un antécédent unique dans E. |
Soient E et F deux espaces vectoriels et E de dimension finie et soit f une application linéaire de , on a alors :
bijective .
Remarque
La démonstration de la proposition 4 est immédiate :
f est bijective donc å injective : (proposition 1)
å surjective : (proposition 2)
Or .
Conséquences
· Si alors
· Si et si alors
Soit f est injective.
· Si , f bijective f injective f surjective.
« Une application linéaire est appelée endomorphisme.
« Une application linéaire bijective de est appelée isomorphisme.
« Une application linéaire bijective de est un automorphisme ou endomorphisme bijectif.
Exemple
Soit définie par . f est-elle surjective ? bijective ? Réponse.