Remarques
«
est orthogonal à tout vecteur
. En effet,
.
« Inversement, si
est orthogonal à tout vecteur de E, alors
. En effet, si
est orthogonal à tout vecteur de E, alors en particulier
et donc
.
«
est orthogonal à
si et seulement si
, c’est-à-dire si et seulement si
.
3.2
Recherche de vecteurs orthogonaux
Dans le plan, il est parfois utile de savoir trouver
rapidement les coordonnées d’un vecteur
orthogonal à un vecteur quelconque
.
Soit
orthogonal à
.
Alors
.
Si on suppose
,
alors on a
.
L’ensemble des vecteurs orthogonaux à
est donc défini comme :
En particulier, si on pose
,
alors
est orthogonal à
.
De même,
est orthogonal à
.
Exemple
Soit
.
Alors
est orthogonal à
:
.
3.4
Ensembles orthogonaux
3.5 Projecteur orthogonal
Soit
espace euclidien. Considérons une direction définie par un vecteur
. Soit
. Cherchons à caractériser la projection orthogonale de
sur la direction définie par
:
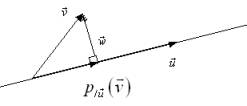
On cherche donc à caractériser le vecteur
par rapport au vecteur
.
Soit
et
tels que par construction l’on ait :
Or
est colinéaire à
donc il peut s’écrire
.
D’autre part, la caractéristique fondamentale de
est que
est orthogonal à
:
