Exemple :
Soit et .
f et g sont des fonctions paires, leur somme définie par est aussi une fonction paire.
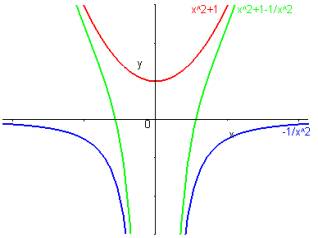
Soit une fonction f, définie sur une partie D de symétrique par rapport à 0 ( ).
Remarque : la seule fonction à la fois paire et impaire est la fonction nulle. En effet, , , donc .
Proposition :
(i) Toute somme finie de fonctions impaires est une fonction impaire.
(ii) Toute somme finie de fonctions paires est une fonction paire.
Exemple :
Soit et .
f et g sont des fonctions paires, leur somme définie par est aussi une fonction paire.

Propositions : Soient f et g définies sur une partie D de symétrique par rapport à 0 ( ).
(i) Si f et g ont même parité, fg est paire. Si elles sont de parité contraire, fg est impaire.
(ii) L’application , si elle existe, est de même parité que f.
(iii) Soit . Si f et g sont paires (respectivement impaires), est paire (respectivement impaire).
(iv) Si f est bijective de D dans D ( ) et impaire, alors sa bijection réciproque est impaire.
(v) Si f est paire, alors est paire quelque soit la fonction h.
(vi) Si f est impaire, et si g paire ou impaire, alors à la même parité que g.
Exemple :
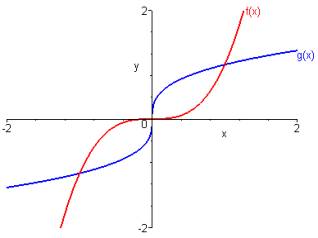
Soit . f est impaire et bijective sur .
Sa fonction réciproque est impaire sur .
Définition :
Soit . S’il existe strictement positif tel que , et , alors la fonction f est dite périodique de période T. On dit aussi que f est T-périodique.
Propriétés :
· Si f est T-périodique, alors , f est nT-périodique.
· Si f et g sont T-périodiques, alors est T-périodique, .
· Si f est T-périodique, alors la fonction , si elle existe, est T-périodique.
· Si f est T-périodique, alors, quelque soit la fonction g, est T-périodique.
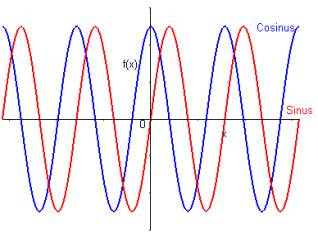
Exemple :
Les fonctions sinus et cosinus sont -périodiques.
Soit f une fonction définie sur un domaine D de symétrique par rapport à 0 ( ).
f est impaire si et seulement si son graphe est symétrique par rapport à l’origine.
Pour , et si existe, on a , d’où et donc .
Ceci signifie que le graphe d’une fonction impaire qui est définie en 0 passe nécessairement par l’origine.
Exemples :
|
(1) |
(2) |
|
|
|
Dans un repère orthonormé, soit une fonction f, définie sur un domaine D de symétrique par rapport à 0 ( ).
f est paire si et seulement si son graphe est symétrique par rapport à .
Exemples :
|
(3) |
(4) |
|
|
|
Soit , le domaine étant tel que ( donné).
f est T-périodique si et seulement si son graphe est invariant par une translation de vecteur avec .
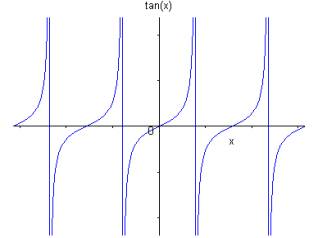
Exemple :
Soit
Soit f une application bijective de D sur .
Les graphes des fonctions f et sont symétrique par rapport à la droite .
Voir § 3.3.2. chapitre 1
Soit une fonction f, définie sur un domaine D de symétrique par rapport à 0.
· Si f est paire (ou impaire), on peut réduire l’intervalle d’étude aux x positifs. Le graphe de la fonction sur D se déduira par symétrie par rapport à Oy (ou 0).
· Si f est T-périodique, on peut réduire l’intervalle d’étude à la seule période T. Le graphe de la fonction sur D se déduira par des translations de T le long de l’axe des x.