Dérivation – Etude de fonctions

6 Théorème des accroissements finis

6.1 Théorème

Théorème des accroissements finis (Généralisation du théorème de Rolle) :

Soit f une fonction vérifiant les conditions suivantes :

- f est définie et continue sur un intervalle fermé ,

- f est dérivable sur ,

Alors il existe au moins une valeur c de l’intervalle ouvert telle que :

! Attention ! Comme pour le théorème de Rolle, il n’y a pas nécessairement unicité de c.

Interprétation géométrique :

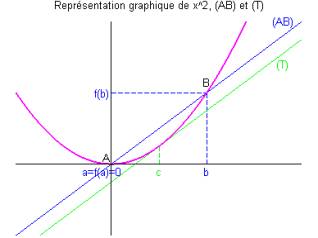
Soient A et B les points de coordonnées respectives et .

est le coefficient directeur de la droite (AB).

est le coefficient directeur de la tangente T à la courbe représentative de f au point c.

_ Le théorème des accroissements finis permet de dire qu’il existe au moins un point c de où la tangente T est parallèle à (AB).

Démonstration

Exemple d’utilisation

Soient f et g deux fonctions définies pour par :

et

Montrons que . Réponse.

6.1.1 Sens de variations des fonctions

Soit f une fonction continue sur et dérivable sur .

Propriétés :

(i) f est constante sur

(ii) f est croissante sur

(iii) f est décroissante sur

Remarque :

Il existe des fonctions pour lesquelles, au voisinage de certains points , f n’est ni croissante ni décroissante, ni même croissante d’un côté et décroissante de l’autre, et qui pourtant admettent une dérivée en ces points.

Voir… !

6.1.2 Inégalités des accroissements finis

Théorème 1 :

Soit f une fonction continue sur et dérivable sur .

S’il existe deux réels m et M tels que , , alors

Théorème 2 :

Soit f une fonction continue sur et dérivable sur .

S’il existe un réel M tels que , , alors

Démonstrations

Conséquence :

D’après ces deux inégalités, pour donné et pour tout , il vient :

- Si , alors

- Si , alors

Ainsi, la fonction f est toujours encadrée, sur l’intervalle , par deux droites d’équations et .

Exemple d’utilisation 14

6.2 Théorème des accroissements finis généralisés

Théorème :

Soient f et g deux fonctions vérifiant les conditions suivantes :

- f et g sont définies et continues sur ,

- f et g sont dérivables sur ,

- ne s’annule pas sur ,

Alors il existe au moins une valeur c de l’intervalle ouvert telle que :

! Attention ! Il n’y a pas nécessairement unicité du point c.

Démonstration

6.3 Règle de L’Hospital

6.4 Théorème du point fixe

Théorème :

Soit f une fonction continue de dans , alors tel que .

Si de plus f est dérivable sur et que , alors c est unique.