Fonctions usuelles

1 Fonctions polynômes élémentaires

1.1 Fonctions polynômes de degré 1

1.1.1 Définition et propriétés

· La fonction polynôme de degré 1 f a une dérivée première constante égale à ; elle est strictement croissante si et strictement décroissante si .

· Il découle de la définition que :

, on a

? L’ accroissement d’une fonction polynôme de degré 1 ( ) sont proportionnels à ceux de la variable .

? est appelé pente de la fonction polynôme de degré 1

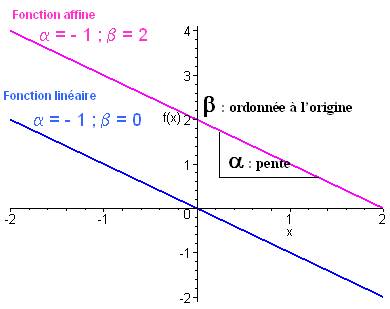
· ; si , on dit que la fonction est linéaire.

· Le graphe d’une fonction polynôme de degré 1 est une droite de pente passant par le point de coordonnées ; est l’ordonnée à l’origine.

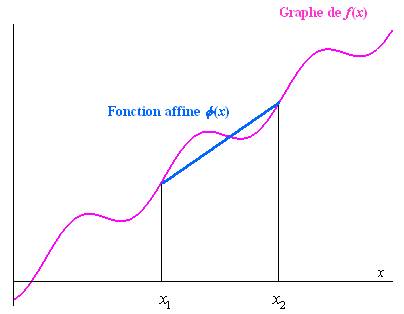
1.1.2 Application : interpolation linéaire

L’interpolation linéaire d’une fonction f dans un intervalle est la fonction polynôme de degré 1 prenant les mêmes valeurs que f aux bornes de l’intervalle :

1.1.3 Un exemple en Biologie

Revoir l’exemple en Biologie présenté au Chapitre 1, §7.

1.2 Polynômes du second degré

1.2.1 Définition et propriétés

La fonction f est continue et dérivable en tout point : .

La dérivée seconde est constante et égale à 2a.

f admet un extremum en : .

Lorsque x tend , f admet pour limite selon le signe de a.

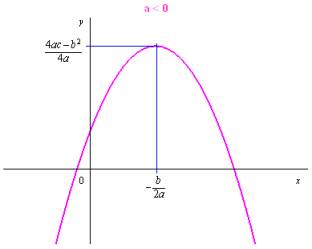
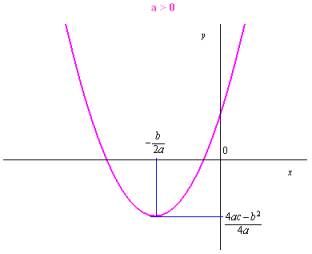
La représentation graphique d’un polynôme du second degré est une parabole :

Nous ne reviendrons pas ici sur la recherche des racines d’un polynôme du second degré.

Rappelons simplement que :

- Si , alors n’admet aucune racine réelle ;

- Si , alors admet une racine double : ;

- Si , alors admet deux racines :

Dans ce cas et .

1.2.2 Un exemple en Biologie

Pour de nombreuses espèces (mammifères, poissons, micro-organismes), il est raisonnable de considérer qu’en première approximation, la relation du taux de croissance de la population avec la température de l’environnement est un polynôme du second degré :

Les valeurs de a, b et c vont dépendre de l’espèce considérée.

Remarquons que d’un point de vue biologie, il faut nécessairement que , ce qui n’est pas nécessairement le cas pour T.

On sait qu’il existe pour chaque individu un optimum de croissance ( ), ainsi que des températures minimale ( ) et maximale ( ) de croissance en deça et au-delà desquelles il n’y a plus de croissance. Ainsi, les paramètres a, b et c doivent vérifier les équations suivantes :

Ce qui implique pour les trois températures cardinales , et :

Chez la bactérie Methylosinus trichosporium, qui est à la fois méthanotrophe et mésophile, on connaît approximativement qui correspond à et (Kevbrina et al., 2001).

D’après le modèle polynomial, on en déduit que doit être égal à 37°C, ce que l’on vérifie presque expérimentalement puisqu’en fait .

On obtient le graphe suivant, où la relation n’est représentée que pour des valeurs positives de µ, c’est-à-dire pour :

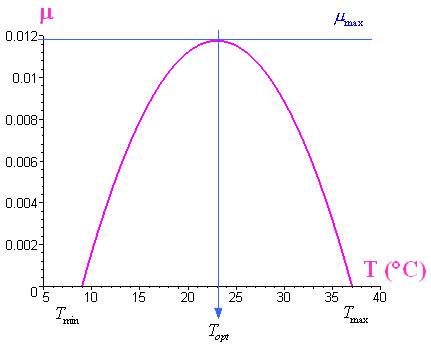
Relation pour la bactérie Methylosinus trichosporium

Données extraites de Kevbrina M.V., Okhapkina A.A., Akhlynin D.S., Kravchenko I.K., Nozhevnikova A.N. et Gal’chenko V.F. (2001) Growth of Mesophilic Methanotrophs at low Temperatures. Microbiology, 70(4), 384-392.

1.3 Fonctions homographiques

1.3.1 Définition et propriétés

· L’ensemble de définition de h est (il faut ).

· (voir Chapitre 2, § 1.5)

· Les limites à droite et à gauche de dépendent du signe de :

- Si , alors et

· La fonction h est continue et dérivable sur :

: le sens de variation de h dépend du signe de

- Si , alors la fonction h est croissante ;

- Si , alors la fonction h est décroissante ;

- Si , la fonction h est constante et égale à

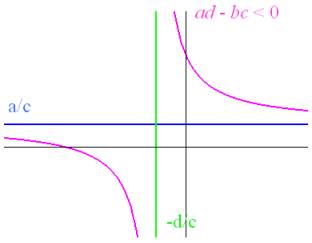
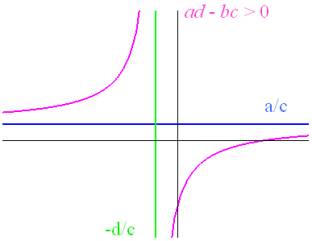
- Si , deux cas de figure peuvent se présenter (voir Figures)

· Le graphe d’une fonction homographique est une hyperbole équilatère, qui admet pour asymptote les deux droites d’équation et ; le point d’intersection des deux asymptotes est un centre de symétrie pour le graphe.

1.3.2 Un exemple en Biologie : d’après Legay et al. (1981), p60

Une réaction enzymatique peut se symboliser par le schéma suivant :

qui se lit : « le substrat S est transformé par l’enzyme E en un produit P ».

Quantitativement, on décrit l’évolution d’une telle réaction par sa cinétique exprimée en terme de vitesse de réaction V :

avec t le temps de réaction

où est la concentration en substrat S et la concentration en produit P.

On peut raisonnablement considérer que la vitesse V suit la relation suivante :

avec et des constantes strictement positives

On suppose vérifiées les conditions suivantes :

A , on a et

, on a :

Mathématiquement, le domaine de définition de V est , mais biologiquement, il faut que . Comme (c’est une concentration), on étudie V sur l’intervalle .

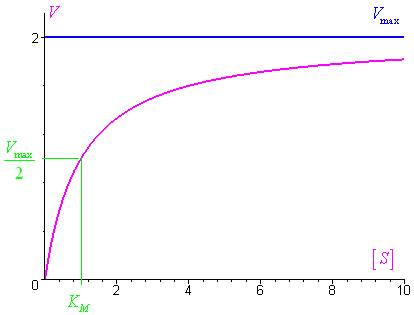
représente la vitesse maximale de réaction. Le graphe de V en fonction de présente une asymptote d’équation .

est égal à la concentration en substrat correspond à une vitesse :

V est continue et dérivable sur :

La fonction V est strictement croissante sur :