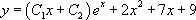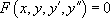.Les équations différentielles d’ordre 2 sont de la forme générale .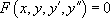
Comme pour les équations différentielles d’ordre 1, on distingue les équations différentielles d’ordre 2 sans et avec second, puis les équations différentielles d’ordre 2 linéaires, sans et avec second membre.
La différence avec les équations différentielles d’ordre 1, tient au fait que la solution générale dépend cette fois-ci de deux constantes d’intégration.
Ainsi, pour déterminer la solution particulière d’un problème donné, il faudra disposer de deux conditions initiales, qui sont le plus souvent : 
et 
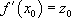, si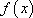 
est une solution de l’équation différentielle.
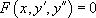
L’astuce consiste ici à poser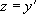 
, ce qui permet de se ramener à 
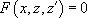, qui est une équation différentielle d’ordre 1.
Ainsi, on résout si c’est possible d’abord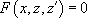 
, ce qui donne 
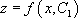; puis on résout 
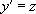, ce qui permet finalement d’obtenir 
.
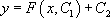Exemple :
« Résoudre l’équation  |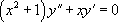
On pose encore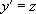 
, d’où 
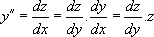ce qui nous ramène à considérer z comme une fonction inconnue de y. On est ainsi ramené à l’équation :
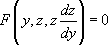avec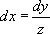 
Exemple :
« Résoudre l’équation  |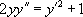
On appelle ainsi une équation différentielle de la forme :
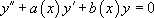
Ces équations ne se résolvent que si l’on dispose d’une solution particulière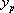 
.
Remarque :
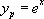est solution particulière de toute équation différentielle de la forme :
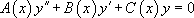
à condition que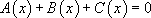 
.
Connaissant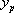 
, on pose 
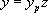, z devenant la nouvelle fonction inconnue de x. Il en résulte :
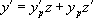
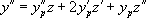
Ainsi :
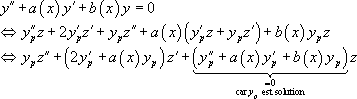
On pose alors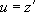 
ce qui ramène à une équation différentielle d’ordre 1 à variables séparables :
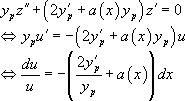
Ainsi,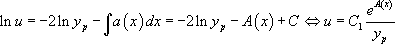 
.
Reste à résoudre 
, c’est-à-dire 
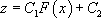, ce qui conduit finalement à la solution générale de l’équation différentielle de départ :
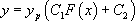
Exemple :
« Résoudre l’équation  |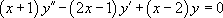
On désigne ainsi une équation différentielle de la forme :
: 
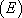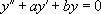avec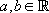 
des constantes
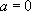
· Si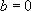 
, alors 
devient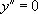 
, ce qui donne 
.
· Si 
, on peut poser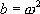 
avec 
, ce qui conduit à 
. Cette équation admet deux solutions particulières simples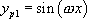 
et 
. La solution générale de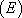 
est donc 
.
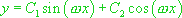· Si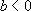 
, on pose alors 
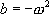avec 
, ce qui conduit à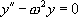 
. Cette équation admet deux solutions particulières simples 
et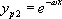 
. La solution générale de 
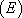est donc 
.
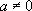
On revient donc à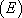 
: 
.
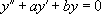En inspirant de ce qui précède, on peut imaginer de chercher des solutions sous la forme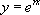 
avec r une constante.
En remplaçant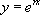 
dans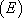 
puis en simplifiant par 
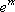, on obtient l’équation :
: équation caractéristique de 
La nature des solutions de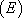 
dépend alors de la nature des solutions de 
.
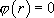On note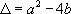 
le discriminant de l’équation caractéristique.
· Si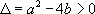 
, alors 
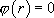admet deux racines réelles distinctes 
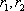, et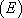 
admet deux solutions particulières 
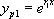et 
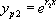. La solution générale de 
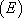est donc 
.
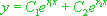· Si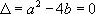 
, alors 
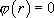admet une racine double 
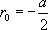et 
admet la solution particulière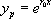 
. En posant 
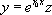, on montre que la solution générale de 
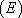est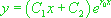 
.
· Si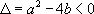 
, alors 
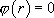admet deux racines complexes conjuguées 
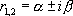. La solution générale de 
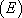s’écrit alors 
.
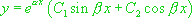Exemple :
« Résoudre l’équation  |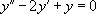
On appelle dans ce paragraphe des équations différentielles de la forme :
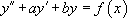
Ces équations ASM se résolvent en deux temps :
(1) On intègre d’abord l’équation SSM (§ 5.3.) ; on obtient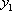 
.
(2) On résout l’équation ASM en recherchant une solution particulièr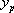e 
de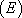 
(voir Chapitre 6 § 6) et dans ce cas 
.
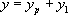Nous allons voir à partir d’un exemple, comment mettre en œuvre la recherche d’une solution particulière.
Considérons l’équation suivante :
: 
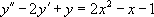
1. Résolution de l’équation SSM : voir exemple ci-dessus :
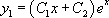
2. On cherche alors une solution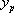 
sous la forme 
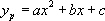,c’est-à-dire une solution particulière de la forme du second membre ; on cherche alors les coefficients a, b, et c pour que 
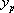soit solution de 
:
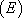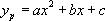
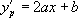
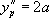
Ainsi :
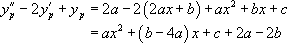
En identifiant,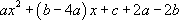 
avec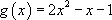 
, on obtient :
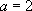
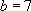
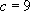
On en déduit que 
est une solution particulière de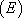 
.
3. On conclut que la solution générale de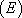 
est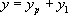 
, c'est-à-dire:
