Une variable aléatoire est dite continue si elle peut prendre toutes les valeurs dans un intervalle donné (borné ou non borné). En règle générale, toutes les variables qui résultent d’une mesure sont de type continu.
Exemples :
Les variables aléatoires,
- le masse corporelle des individus pour une espèce animale donnée,
- taux de glucose dans le sang,
- etc.
sont des variables aléatoires continues.
Dans le cas d’une variable aléatoire continue, la loi de probabilité associe une probabilité à chaque ensemble de valeurs définies dans un intervalle donné. En effet, pour une variable aléatoire continue, la probabilité associée à l’évènement {X = a} est nulle, car il est impossible d’observer exactement cette valeur.
On considère alors la probabilité que la variable aléatoire X prenne des valeurs comprises dans un intervalle [a,b] tel que P(a £ X £ b).
Lorsque cet intervalle tend vers 0, la valeur prise par X tend alors vers une fonction que l’on appelle fonction densité de probabilité ou densité de probabilité.
On appelle densité de probabilité toute application continue par morceaux :
¦: R ® R
x ® f (x)
telle que :
(P1) "x Î R f (x) ³ 0
(P2) f (x) dx = 1 (en supposant que f (x) dx existe)
|
|
Soit une fonction densité de probabilité f(x) : (1) l’aire hachurée en vert correspond à la probabilité P(X < -10) (2) l’aire hachurée en bleu correspond à la probabilité P(+10 <X < +15)
|
| Remarque : | Cette fonction densité de probabilité est une loi de probabilité car l’aire sous la courbe est égale à 1 pour toutes les valeurs de x définies. |
Réciproquement :
Une variable aléatoire X définie sur un univers W est dite absolument continue, s’il existe une fonction densité de probabilité ¦ telle que :
" t Î R P(X < t) = f (x) d
(voir graphe ci-dessus).
Si comme pour les variables aléatoires discrètes, on définit la fonction de répartition de X par :
FX : R ® R
t FX (t) = P( X < t)
alors la relation entre la fonction de répartition et la fonction densité de probabilité f(x) est la suivante :
" t Î R FX (t) = P( X < t) = f (x) dx
La fonction de répartition FX (t) est la primitive (voir cours d’analyse) de la fonction densité de probabilité f (x), et permet d’obtenir les probabilités associées à la variable aléatoire X, en effet :
Soit X une variable aléatoire absolument continue de densité f et de fonction de répartition FX , alors :
(P1) P(a £ X £ b) = FX (b) - FX (a) = f(x)dx avec a < b
(P2) " a Î R P(x = a) = 0 si f est continue à droite du point a.
|
Voici pourquoi : (P1 ) P(a £ X £ b) = P(X < b) - P(X < a) = FX (b) - FX (a) d’où f(x) dx - f(x) dx = f(x) dx
(P2) Si f est continue sur un intervalle de la forme [a, a+h] avec h ® 0+ alors, P(a £ X £ a+ h) = f(x) dx = h f (a+q h) avec (0 <q <1) (théorème des accroissements finis) Ainsi lorsque h ® 0+ : f (a+q h) ® f(a) et h f (a+q h) ® 0 d’où P(a £ X £ a+ h) ® P(X = a) = 0 |
| Remarque : | La propriété P2 implique que P(X £ t) = P(X < t). |
La fonction de répartition correspond aux probabilités cumulées associées à la variable aléatoire continue sur l’intervalle d’étude (graphe ci-dessous).
|
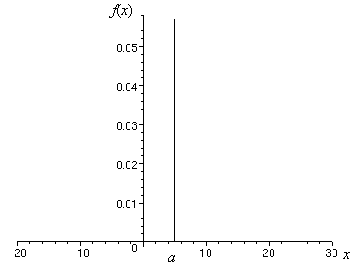
Fonction densité de probabilité f(x) |
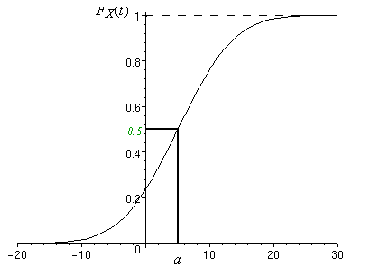
Fonction de répartition FX |
L’aire hachurée en vert sous la courbe de la fonction densité de probabilité correspond à la probabilité P(X < a) et vaut 0,5 car ceci correspond exactement à la moitié de l’aire totale sous la courbe. Cette probabilité correspond à la valeur de la fonction de répartition au point d’inflexion de la courbe (voir cours analyse).
Les propriétés associées à la fonction de répartition sont les suivantes :
Soit FX la fonction de répartition d’une variable aléatoire absolument continue X alors :
(P1) FX est continue sur R, dérivable en tout point où ¦ est continue et alors ’ = f
(P2) FX est croissante sur R
(P3) FX est à valeurs dans [0,1]
(P4) FX (t) = 0 et FX (t) = 1
|
Voici pourquoi : (P1) résulte de la relation suivante FX (t) = f (x) dx (P2) FX ‘ = f est donc positive sur R (P3) Evident (P4) f (x) dx tend vers 0 quand t ® -¥ |
Exemple :
|
Dans une population de canards colverts, lors d’une leur lieu de repos. Ainsi à t = 0, la surface de l’étang regagne l’étang entre les temps t1 et t2 (en minutes)
Canards colverts Anas platyrhynchos |
alerte, l’ensemble des individus quittent est déserte et la probabilité qu’un canard est donnée par : avec qui représente la fonction densité de probabilité. La primitive de , , fonction de répartition est de la forme :
(voir démonstration)
|
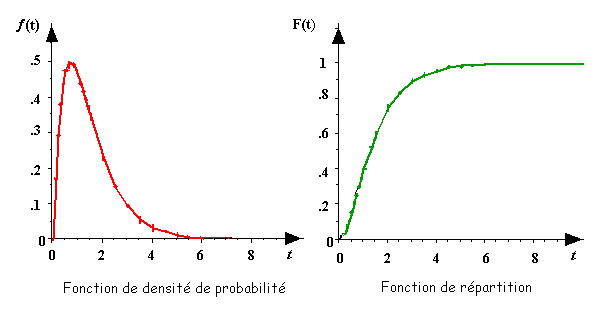
L’évolution de la recolonisation de l’étang par les canards colverts en fonction du temps est donnée par la courbe rouge. On observe ainsi que plus de 50 % des canards se posent sur l’étang au cours des 2 premières minutes qui suivent l’alerte. Au bout de 7 minutes, tous les canards ont regagné l’étang. La distribution des probabilités cumulées est donnée sur la courbe verte.
