Exemples :
Les variables aléatoires,
- le nombre de petits par porté
pour une espèce animale donnée (chat, marmotte, etc.),
- le nombre de bactéries dans 100
ml de préparation,
- le nombre de mutations dans une séquence d’ADN de 10 kb,
etc.
sont des variables aléatoires discrètes.
2.2 Loi de probabilité
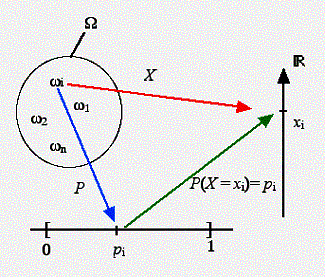
Une variable aléatoire est caractérisée par l’ensemble des
valeurs qu’elle peut prendre et par l’expression mathématique de la probabilité
de ces valeurs. Cette expression s’appelle la
loi de probabilité (ou distribution de probabilité) de la variable
aléatoire.
| Remarque : |
Afin de simplifier l’écriture, nous noterons pour la suite du cours : |
|
P({X = xi}) équivalent à P(X=xi) ou pi
|
Exemple :
Dans le cas de la constitution d’une fratrie de deux
enfants, si l’on fait l’hypothèse que la probabilité d’avoir un garçon est
égale à celle d’avoir une fille (1/2), alors la distribution de
probabilité ou loi
de probabilité du nombre de filles dans une fratrie de deux enfants
est :
|
Ensemble des
évènements possibles
W
|
Valeurs de la
variable aléatoire
X
|
Probabilités
associées
à la variable X
P(X=xi) ou pi
|
|
G et G
F et G ou G et F
F et F
|
0
1
2
|
1/4
1/2
1/4
|
Si P(F)= P(G)=1/2, alors
(1) P[(F Ç G) È (G Ç F)]
= P(F Ç G) + P(G Ç
F) Propriétés d’additivité
avec (F Ç G) Ç (G Ç F) = Æ évènements incompatibles
(2) P(F Ç G) =
P(F)P(G) Propriété d’indépendance
d’où P[(F Ç
G) È
(G Ç
F)] = P(X =1) = (1/2x1/2)+(1/2x1/2) = 1/2
| Remarque : |
Une loi de probabilité n’est établie que si
, la somme étant étendue à tous les indices i. |
|
|
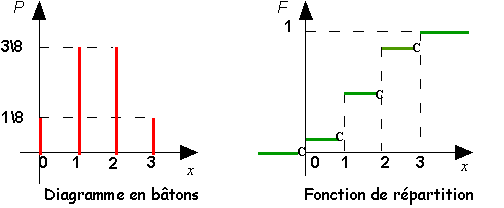
2.3 Fonction
de répartition
Concrètement la fonction de répartition correspond à la distribution des
probabilités cumulées. Le plateau atteint par la fonction de
répartition correspond à la valeur de probabilité 1 car
.
L’importance pratique de la fonction de répartition est
qu’elle permet de calculer la probabilité de tout intervalle dans R.
Les propriétés associées à la fonction de
répartition sont les suivantes :
Soit FX la fonction de répartition d’une variable aléatoire discrète X
alors :
(P1) "t Î R 0 £ FX (t) £ 1
(P2) FX est croissante sur R
(P3)
FX (t) = 0 et
FX (t) = 1
(P4) si a £ b P (a £ X £ b) = FX (b) - FX (a)