Interprétation géométrique
Considérons la fonction f définie sur par .
Voici la courbe représentative de f :
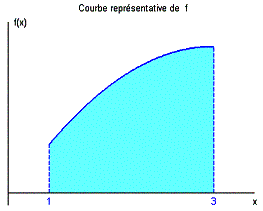
Désignons par l’aire en bleu clair sous la courbe bleue.
Découpons l’intervalle en n intervalles plus petits de longueur :
Soit une fonction admettant une primitive sur I.
Soient F et G deux primitives de f sur I. Alors, avec .
Ainsi, .
Ce nombre est donc indépendant du choix de la primitive.
Définition 1 :
Soit une fonction admettant une primitive sur I et F l’une d’entre elles.
Soient . Alors le nombre est appelé intégrale de f sur .
Remarque : On peut remarquer que ne dépend pas du choix de la primitive F parmi l’infinité des primitives de f.
Considérons la fonction f définie sur par .
Voici la courbe représentative de f :

Désignons par l’aire en bleu clair sous la courbe bleue.
Découpons l’intervalle en n intervalles plus petits de longueur :
|
(A)
|
(B)
|
 |
 |
|
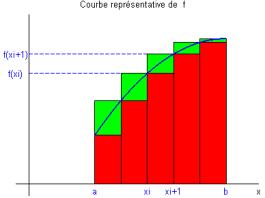
avec 5 intervalles entre a et b
|
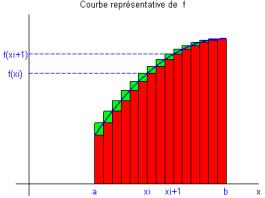
avec 15 intervalles entre a et b
|
· On désigne alors par l’expression suivante :
représente alors la somme de tous les rectangles rouges
Il est clair que et que est d’autant plus proche de que est petit (Fig. A).
· On désigne alors par l’expression suivante :
représente alors la somme de tous les rectangles verts.
Il est clair que et que est d’autant plus proche de que est petit (Fig. B).
Par conséquent et on définit l’intégrale de f sur I par :
désigne un infiniment petit :
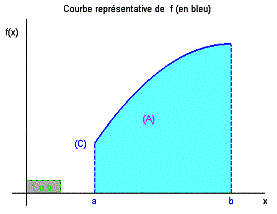
Définition 2 (Intégrale et Aire) :
Soit une fonction positive admettant une primitive sur et (C) sa courbe représentative.
L’aire du domaine (A) délimitée par :
- la courbe (C)
- l’axe des abscisses
- les droites d’équations et
est , exprimée en unités d’aire (u.a.). Voir figure ci-dessous.
 d’après Misset et al.
d’après Misset et al.
Définition 3 :
Soit une fonction admettant une primitive sur I et F l’une d’entre elles.
L’intégrale de f sur (définition 1) se note . Ainsi :
que l’on note aussi
se lit « somme de a à b de ».
Historiquement, on doit une telle définition à Riemann qui donna son nom aux sommes dites de Riemann . On parle alors d’intégrale de Riemann.
La façon dont nous venons de définir l’intégrale d’une fonction sur un intervalle revient à minorer ou à majorer l’intégrale par une somme de rectangles ; on parle de méthode des rectangles. Nous verrons ultérieurement d’autres méthodes d’approximation numérique des intégrales (chapitre 5, § 5).
Remarque : est un nombre réel (voir définitions 1 et 2). Pour des raisons qui restent encore mystérieuses on dit que « l’on intègre f par rapport à la variable x sur l’intervalle ».
Bien évidemment, le symbole x n’a pas de rôle particulier (c’est une variable « muette ») et représente la même quantité que ou .
Définition 4 :
Soit une fonction admettant des primitives sur I.
On note l’ensemble des primitives de f.
Proposition :
Soient une fonction admettant des primitives sur I et .
La fonction F définie sur I par l’intégrale est l’unique primitive de f sur I qui s’annule en .
Proposition :
Soient f et g deux fonctions continues sur . :
Remarque :
On dit que l’intégrale d’une somme est la somme des intégrales.
Propositions :
(i) Soit f une fonction continue sur .
Si , (resp. ), alors (resp. ).
(ii) Soit f une fonction continue sur . Si , , alors :
Par extension, si f, g et h sont trois fonctions intégrables sur telles que sur , alors .
Ainsi, si on ne connaît pas de primitive de la fonction g, on peut malgré tout obtenir un encadrement de son intégrale sur .
Proposition :
Soit f une fonction continue sur . Alors :
Ce théorème découle immédiatement de la définition de l’intégrale. F étant une primitive de f sur , pour tout , on a : .
Exemple :