Chapitre 3 : Variables aléatoires

 

1         Introduction

 

Dans la plupart des phénomènes aléatoires, le résultat d’une épreuve peut se traduire par une « grandeur » mathématique, très souvent représentée par un nombre entier ou un nombre réel. La notion mathématique qui représente efficacement ce genre de situation concrète est celle de  variable aléatoire (notée également v.a.). Ainsi le temps de désintégration d’un atome radioactif, le pourcentage de réponses « oui » à une question posée dans un sondage ou

le nombre d’enfants d’un couple sont des exemples de variables aléatoires.

 

Remarque : On se limitera ici au cas des variables aléatoires réelles (les entiers faisant bien sûr partie des réels).

 

Etant donné un espace probabilisé d’espace fondamental W et de mesure de probabilité P,

on appelle variable aléatoire sur cet espace, toute application X de W dans R telle que :

                                   X:    e (W)  ®  ­R

                                            w  ® X (w)

 

           

                             

 

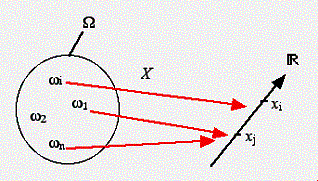
A chaque évènement élémentaire w de W correspond un nombre réel x associé à la variable aléatoire X.  Comme l’indique le graphe, il n’y a pas obligatoirement autant de valeurs possibles prises par la variable aléatoire X que d’évènements élémentaires. La valeur x correspond à la réalisation de la variable X pour l’évènement élémentaire w.         

 

Exemple :

Si l’on considère la constitution d’une fratrie de deux enfants, l’espace fondamental est constitué des évènements élémentaires suivant :

                                   W = {GG, GF, FG, FF}

 Les valeurs possibles prises par la variable aléatoire X, « nombres de fille dans la famille »   sont :           X (W) = {0, 1, 2}