Chapitre 2 : Probabilités
3 Probabilités
Le passage d’une description de type ensembliste des phénomènes aléatoires à l’élaboration d’un véritable modèle mathématique se fait en introduisant les mesures de probabilité.
3.1 Définitions
3.1.1 Concept mathématique
On appelle probabilité P toute application de l’ensemble des évènements W dans l’intervalle [0,1], tel que : P : e (W) ® [0,1]
satisfaisant les propriétés (ou axiomes) suivantes
(P1) "A Î e(W) P(A) ³ 0
(P2) P(W) = 1
(P3) "A, B Î e(W) si AÇB = Æ alors P(A ÈB)=P(A) + P(B)
| Remarque : |
Le concept mathématique de probabilité modélise les notions intuitives de proportion et de fréquence. |
|
Si l’on avance que la probabilité d’être immunisé contre la tuberculose est de 0,8, on modélise le fait qu’environ 80 % de la population est immunisé contre la tuberculose. |
3.1.2 Probabilités combinatoires
Soit W un espace fondamental fini constitué de N évènements élémentaires sur lequel on fait l’hypothèse d’équiprobabilité de réalisation des N évènements élémentaires. On suppose ainsi que tous les évènements élémentaires ont « la même chance » de se réaliser. Dans ce cas la probabilité pi d’un évènement élémentaire quelconque wi est telle que :
avec pi = P(wi )
 satisfaisant (P1) avec "i pi ³ 0
satisfaisant (P1) avec "i pi ³ 0
(P2)
= 1
Soit A un évènement quelconque constitué de k évènements élémentaires de W, on en déduit :
avec
Cette formule s’énonce souvent comme :
Cette formule permet de ramener les calculs de probabilités à des décomptes d’évènements élémentaires effectués par des techniques d’analyse combinatoire qui ne sont pas des probabilités.
Exemples :
(1) En tapant 5 lettres au hasard sur une machine à écrire (possibilité de taper plusieurs fois sur la même touche), la probabilité d’obtenir le mot « lutte » est d'une chance sur 12 millions. En effet il y a exactement 11 881 376 mots de 5 lettres possibles (Voir Arrangement avec répétition).
(2) La probabilité d’obtenir un multiple de trois lors du lancé d’un dé à 6 faces, non pipé est : A = {3,6} d’où P(A) = 2/6 = 1/3 avec k =2 et pi =1/6
3.1.3 Loi des grands nombres
Si l’on répète N fois une expérience dans laquelle la probabilité d’apparition d’un
évènement A est P, la fréquence de cet évènement au cours des N expériences,
tend
vers P lorsque N tend vers l’infini.
Lorsque le nombre d’épreuves augmente indéfiniment, les fréquences observées tendent vers les probabilités et les distributions observées vers les lois de probabilité.
Exemple :
Lors d’un croisement entre plantes hétérozygotes Aa pour un caractère à dominance stricte (allèle A, forme sauvage et allèle a, forme mutée), on examine successivement deux échantillons de plantes résultant de ce croisement.
|
|
N=40 fleurs
|
N=1000 fleurs
|
|
|
Effectifs
|
Fréquences
|
Effectifs
|
Fréquences
|
Probabilités
attendues
|
|
Phénotype sauvage
|
29
|
0,725
|
754
|
0,754
|
0,750
|
|
Phénotype
|
11
|
0,275
|
246
|
0,246
|
0,25
|
Il est aisé de vérifier que les fréquences pour les deux phénotypes possibles sont plus proches des probabilités attendues sous le modèle de croisement mendélien pour l’échantillon de très grande taille. L’écart entre les fréquences observées et les probabilités attendues peut être testé à l’aide du test du khi-deux.
3.1.4 Espace probabilisé
Nous définirons un espace probabilisé en utilisant l’axiomatique de Kolmogorov,
Définition 1 :
On appelle probabilité sur (W, C) une application P de C dans l’intervalle [0,1] telle que :
• P(W)=1
• pour tout ensemble dénombrable d’évènements incompatibles 2 à 2, on a :
Définition 2 :
On appelle espace probabilisé, le triplet (W, C, P)
Ainsi un espace probabilisé désigne un espace fondamental et ses évènements, muni d’une mesure de probabilités.
3.2 Propriétés des probabilités
Des axiomes précédents découlent les propriétés additives des probabilités, d’usage permanent.
3.2.1 Additivité
• Cas d’évènements incompatibles
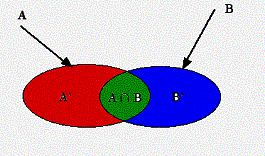
Si A et B sont deux évènements quelconques, alors :
P(A È B) = P(A) + P(B) - P(AÇ B)
|
Voici pourquoi :
A et B étant deux évènements quelconques,
(AÇB) ¹ Æ, ces évènements peuvent se décomposer comme la réunion de deux évènements incompatibles :
|
Alors:
1. A = A’È (A Ç B) avec A’Ç (A Ç B) = Æ
alors P(A) = P(A’) + P(A Ç B)
et P(A’) = P(A) - P(A Ç B)
2. B = B’È (A Ç B) avec B’Ç (A Ç B) = Æ
d’où P(B’) = P(B) - P(A Ç B)
3. P(A È B) = P(A’) + P(A Ç B) +P(B’)
d’où P(A È B) = P(A) + P(B) - P(A Ç B)
|
Exemple :
Dans l’exemple du lancer d’un dé à 6 faces, non pipé, on considère l’évènement A « le résultat est pair » et l’évènement B « le résultat est un multiple de trois ».
On a alors :
A = {2,4,6} et B = {3,6} donc AÈ B = {2,3,4,6} et A Ç B = {6}
avec P(A) = 3/6 P(B) = 2/6 P(AÈ B) = 4/6 P(A Ç B) = 1/6
on vérifie alors que : P(A È B) = P(A) + P(B) - P(AÇ B) = 3/6 + 2/6 - 1/6 = 4/6
3.2.2 Evènement contraire
Si A est un évènement quelconque, alors
|
Voici pourquoi :
Nous avons vu précédemment que
A È
= W et A Ç
= Æ Propriétés de la réunion et de l’intersection
P( A È
) = P(A) + P(
) Propriétés d’additivité des probabilités
d’où P(W) = 1 = P(A) + P(
) ainsi P(
) = 1 - P(A)
|
Exemple :
La probabilité lors du lancer d’un dé non pipé d’obtenir « plus de 2 » se traduit par
A = {3,4,5,6} et
= {1,2} d’où P(A) = 1 – P(
) = 1 – 2/6 = 4/6 = 2/3
| Remarque : |
L’application de cette propriété est très utile lorsque le nombre d’évènements élémentaires de A, k , est important et que le calcul des probabilités pi est fastidieux (cas de la loi de Poisson). |
|
|
3.2.3 Evènement impossible
|
Voici pourquoi :
Nous avons vu précédemment que
Æ È W = W élément neutre
P(Æ È W) = P(Æ) + P(W) Propriétés d’additivité des probabilités
d’où P(W) = P(Æ) + P(W) ainsi P(Æ) = 0
|
3.2.4 Inclusion
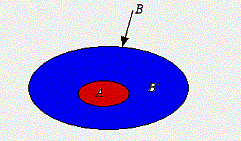
Si A Ì B alors P(A) £ P(B)
|
Voici pourquoi :
si B = B’ È A avec B’ Ç A = Æ
alors P(B)= P(B’ È A) = P(B’) + P(A)
d’où P(A) £ P(B)
avec P(A) = P(B) lorsque P(B’) = 0
|
|
3.3 Indépendance statistique
3.3.1
Définition
L’hypothèse d’indépendance entre évènements et plus généralement entre épreuves successives est un préalable lors de l’établissement des lois de probabilités
On dit que deux évènements A et B sont indépendants si l’on a :
P(A Ç B) = P(A) P(B)
Ainsi si A et B sont deux évènements statistiquement indépendants, la probabilité de la réalisation conjointe de ces deux évènements est le produit de leur probabilité respective.
| Remarque : |
.Il ne faut pas confondre évènements indépendants et évènements incompatibles. |
|
|
Supposons A et B à la fois indépendants et incompatibles. On a alors :
P(A Ç B) = P(A)P(B) indépendants
P(A Ç B) = P(Æ) = 0 incompatibles
d’où nécessairement P(A) = 0 ou P(B) = 0
Exemples :
(1) Dans l’exemple du lancer d’un dé à 6 faces, non pipé, les deux évènements : A « le résultat est pair » et B « le résultat est un multiple de trois » sont statistiquement indépendants.
En effet, soit A = {2,4,6} B = {3,6} A Ç B ={6}
ainsi P(A) = 3/6 P(B) = 2/6 P(A Ç B) = 1/6
on vérifie alors que : P(A Ç B) = P(A) P(B) = 3/6 X 2/6 = 6/36 = 1/6
(2) Si l’on considère une famille de deux enfants, les deux évènements : A « enfants de sexe différent » et B « au plus une fille » ne sont pas statistiquement indépendants.
En effet, l’espace probabilisé W, contient 4 évènements élémentaires (si l’on considère une famille ordonnée),
W = A È B = {GG, GF, FG, FF}
avec A = {GF, FG}, B = {GG, GF, FG} et A Ç B = {GF, FG}
d’où sous l’hypothèse d’équiprobabilité : P(A) = 1/2, P(B) = 3/4 et P(A Ç B) = 1/2
On vérifie alors que : P(A Ç B) ¹ P(A) P(B) = 1/2 X 3/4 = 3/8 ¹ 1/2
(3) Quand est-il si vous considérez une famille de trois enfants ? Réponse.
3.3.2 Propriétés
Les propriétés associées à l’indépendance sont :
(1) si A est un évènement quelconque,
A et Ω sont indépendants : A Ç Ω = A élément neutre
P(A Ç Ω) = P(A)P(Ω) = P(A) car P(Ω) = 1
A et ø sont indépendants : A Ç Æ = Æ élément absorbant
P(A Ç Æ) = P(A)P(Æ) = P(Æ) car P(Æ) = 0
(2) si A et B sont deux évènements quelconques,
A et B sont indépendants si et seulement si A et
(
et B) ou sont indépendants (démonstration).
A et B sont indépendants si et seulement si
et
le sont.
3.3.3 Généralisation à n évènements
n évènements (n ³ 2) , A1,A2 ,…,Ai,.., An sont dit indépendants dans leur ensemble
(ou mutuellement indépendants) si on a :
P(A1 Ç A2 Ç…Ç Ai Ç… Ç An ) = P(A1) x P(A2) x …x P(Ai) x….x P(An)
| Remarque : |
n évènements peuvent être indépendants deux à deux, |
|
[P(Ai Ç Aj) = P(Ai) x P(Aj)] avec i ¹ j sans être indépendants au sens de la définition ci-dessus. |
Exemple :
On jette deux dés non pipés et on considère les évènements suivants :
A1 « le premier dé donne un nombre pair »
A2 « le deuxième dé donne un nombre pair »
A3 « la somme des deux lancers est paire »
Le nombre d’événements élémentaires est :
card (W )= 36 (voir arrangements avec répétitions avec p = 2 et n = 6)
Les 3 évènements A1, A2 et A3 sont 2 à 2 indépendants mais ne sont pas indépendants dans leur ensemble. En effet :
|
|
Les probabilités associées aux 3 évènements sont :
P(A1)= 1/2 ; P(A2)=1/2 ; P(A3)=1/2
P(A1 Ç A2) = 9/36 = 1/4 = P(A1)P(A2)
P(A1 Ç A3) = 9/36 = 1/4 = P(A1)P(A3)
P(A2 Ç A3) = 9/36 = 1/4 = P(A2)P(A3)
P(A1 Ç A2 Ç A3) = 9/36 = 1/4
¹ P(A1)P(A2)P(A3) = 1/8
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
|
|
|
|
|
|
|
|
|
Les cases grisées représentent les évènements élémentaires réalisés dans le cadre soit
A1Ç A2 ou A1Ç A3 ou A2Ç A3 ou A1Ç A2Ç A3.
![]() satisfaisant (P1) avec "i pi ³ 0
satisfaisant (P1) avec "i pi ³ 0