Le dernier niveau de description statistique est le résumé numérique d’une distribution statistique par des indicateurs numériques ou paramètres caractéristiques.
| Remarque : | Ces derniers représentent une transition entre la statistique purement descriptive et l’estimation des paramètres qui caractérisent les distributions de probabilité (chapitre 6). |
Ces paramètres ont pour objectif dans le cas d'un caractère quantitatif de caractériser l’ordre de grandeur des observations.
Soit un échantillon de n valeurs observées x1, x2, ….,xi,….,xn d’un caractère quantitatif X,
on définit sa moyenne observée comme la moyenne arithmétique des n valeurs :
| Remarque : | Une des propriétés de la moyenne arithmétique est que la somme des écarts à la moyenne est nulle: |
Si les données observées xi sont regroupées en k classes d’effectif ni (caractère
continu regroupé en classe ou caractère discret), il faut les pondérer par les
effectifs correspondants:
avec
Exemples :
(1) Dans le cas de l’étude du dimorphisme sexuel de la gélinotte huppée, la longueur moyenne de la rectrice principale du mâle juvénile est :
§ dans le cas des données non groupées :
158,9 mm
§ dans le cas des données groupées où les valeurs xi correspondent aux valeurs médianes des classes,
7 960 d’où 159,2 mm (voir graphe)
(2) Quel est le nombre moyen de galles par feuille pour la cécidomyie du hêtre ? Réponse.
| Remarque : | La moyenne obtenue après regroupement des données en classe dans l’exemple de la longueur de la rectrice centrale diffère légèrement en raison d’une perte d’information. |
|
Si l’échantillonnage n’est pas de type aléatoire simple, les deux moyennes peuvent être très différentes. |
La médiane, Me, est la valeur du caractère pour laquelle la fréquence cumulée est égale à 0,5 ou 50%. Elle correspond donc au centre de la série statistique classée par ordre croissant, ou à la valeur pour laquelle 50% des valeurs observées sont supérieures et 50% sont inférieures.
• Dans le cas où les valeurs prises par le caractère étudié ne sont pas regroupées en classe,
• si n est impair, alors n = 2m + 1 et la médiane est la valeur du milieu Me = xm+1.
• si n est pair, alors n = 2m et une médiane est une valeur quelconque entre xm et xm+1. Dans ce cas il peut être commode de prendre le milieu.
• Dans le cas où les valeurs prises par le caractère étudié sont groupées en classe, on cherche la classe contenant le ne/2 individu de l’échantillon. En supposant que tous les individus de cette classe sont uniformément répartis à l’intérieur, la position exacte du ne/2 individu de la façon suivante par interpolation linéaire :
(voir démonstration géométrique)
avec
xm : limite inférieure de la classe dans laquelle se trouve le ne/2 individu (classe médiane).
xm+1 : limite supérieure de la classe dans laquelle se trouve le ne/2 individu (classe médiane).
ni : effectif de la classe médiane
Ni. : effectif cumulé inférieur à xm
n : taille de l’échantillon
Exemple :
(1) Dans le cas de la distribution de la longueur de la rectrice centrale de la gélinotte hupée, la valeur de la médiane est :
§ Cas des données non groupées :
n = 50 donc Me Î [x25, x26]
soit Me Î [158mm, 159mm] ou Me =158,5mm
§ Cas des données groupées :
n=50, la 25ème valeur se situe dans la classe [155-160[ qui contient les individus de 12 à 28.
d’où avec Lm = 155 mm, fm= 17 individus, fmcum. = 11 individus et i = 5mm
Me = = 159,11 mm d’où Me = 159,1 mm (voir graphe)
(2) Quelle est la valeur de la médiane dans le cas de la répartition du nombre moyen de galles par feuille pour la cécidomyie du hêtre ? Réponse.
| Remarque : | La médiane ne s’applique qu’aux échelles ordinales, d’intervalles et de rapport, car elle nécessite un ordre linéaire entre les variables. |
Si la distribution des valeurs est symétrique, la valeur de la médiane est proche de la valeur de la moyenne arithmétique.
Me »
Le mode, Mo d’une série statistique est la valeur du caractère la plus fréquente
ou dominante dans l'échantillon. Le mode correspond à la classe de fréquence maximale
dans la distribution des fréquences.
On peut identifier le mode comme la valeur médiane de la classe de fréquence maximale ou bien effectuer une interpolation linaire pour obtenir la valeur exacte du mode comme suit :
(voir démonstration géométrique)
avec
xm : limite inférieure de la classe d’effectif maximal
i : intervalle de classe (xm+1 – xm)
: Ecart d’effectif entre la classe modale et la classe inférieure la plus proche
: Ecart d’effectif entre la classe modale et la classe supérieure la plus proche
Exemple :
(1) Dans le cas de la distribution de la longueur de la rectrice centrale de la gélinotte huppée, la valeur du mode est :
§ Valeur approchée :
La classe de fréquence maximale est [155,160[ avec ni = 17 d’où Mo = 157,5 mm
§ Valeur exacte :
Mo = = 159,44 mm d’où Mo = 159,4 mm (voir graphe)
avec xm = 155 mm, Di = 17-9 = 8 , Ds = 17-16 = 1 et i = 5mm
| Remarque : | Une distribution de fréquences peut présenter un seul mode (distribution unimodale) ou plusieurs modes (distribution bi ou trimodale). |
Si la distribution des valeurs est symétrique, la valeur du mode est proche
de la valeur de la moyenne arithmétique.
Mo »
|
|
Avantages |
Inconvenients |
|
Moyenne arithmétique |
- Facile à calculer, - Répond au principe des moindres carrés. |
- Fortement influencée par les valeurs extrêmes de la v.a., - Représente mal une population hétérogène (polymodale). |
|
Médiane
|
- Pas influencée par les valeurs extrêmes de la v.a., - Peu sensible aux variations d’amplitude des classes, - Calculable sur des caractères cycliques (saison, etc.) où la moyenne a peu de signification. |
- Se prête mal aux calculs statistiques, - Suppose l’équi-répartition des données - Ne représente que la valeur qui sépare l’échantillon en 2 parties égales. |
|
Mode |
- Pas influencée par les valeurs extrêmes de la v.a., - Calculable sur des caractères cycliques (saison, etc.) où la moyenne a peu de signification, - Bon indicateur de population hétérogène. |
- Se prête mal aux calculs statistiques, - Très sensible aux variations d’amplitude des classes, - Son calcul ne tient compte que des individus dont les valeurs se rapprochent de la classe modale. |
Exemples :
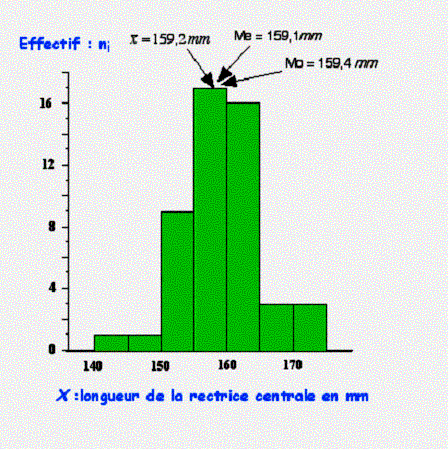
Représentation graphique des trois indices de position sur l’exemple de la distribution de la longueur de la rectrice centrale de la gélinotte huppée.

Dans le cas où le caractère étudié se distribue selon une loi normale Laplace-Gauss,
alors,
la moyenne , la médiane Me et le mode Mo prennent la même valeur.
Il existe d’autres paramètres de position comme la moyenne quadratique ou la moyenne géométrique qui ne seront pas développés dans ce cours.
Ces paramètres ont pour objectif dans le cas d'un caractère quantitatif de caractériser la variabilité des données dans l’échantillon.
Les indicateurs de dispersion fondamentaux sont la variance observée et l’écart-type observé.
Soit un échantillon de n valeurs observées x1, x2, ….,xi,….,xn d’un caractère quantitatif X et soit sa moyenne observée. On définit la variance observée notée s2 comme la moyenne arithmétique des carrés des écarts à la moyenne.
Pour des commodités de calcul, on se sert du théorème de Kœnig que nous démontrons dans un cas particulier.
![]() Voici pourquoi :
Voici pourquoi :
Soit
d’où or
d’où
ainsi
La formule de la variance qui résulte du théorème de Kœnig est donc :
Dans le cas de données regroupées en k classes d'effectif ni (variable continue regroupée en classes ou variable discrète), la formule de la variance est la suivante :
Pour des commodités de calcul, on utilisera la formule développée suivante :
avec
L’écart-type observé correspond à la racine carrée de la variance observée:
Exemple :
(1) Dans le cas de l’étude du dimorphisme sexuel de la gélinotte huppée, la variance observée de la longueur de la rectrice centrale du mâle juvénile est :
§ cas des données non groupées :
et 158,86 mm
= 36,44 d’où s2=36,44 et s =6,04 mm
§ cas des données groupées :
et 159,20 mm
= 35,61 d’où s2=35,61 et s= 5,97 mm
(1) Quelle est la variance et l’écart-type observée du nombre moyen de galles par feuille pour la cécidomyie du hêtre ? Réponse.
| Remarque : | De part sa définition, la variance est toujours un nombre positif. Sa dimension est le carré de celle de la variable. Il est toutefois difficile d’utiliser la variance comme mesure de dispersion car le recours au carré conduit à un changement d’unités. |
|
Elle n’a donc pas de sens biologique direct contrairement à l'écart-type qui s’exprime dans les mêmes unités que la moyenne. |
La variance et l’écart-type observée sont des paramètres de dispersion absolue qui mesurent la variation absolue des données indépendamment de l’ordre de grandeur des données.
Le coefficient de variation noté C.V. est un indice de dispersion relatif prenant en compte ce biais et est égal à :
C.V. =
Exprimé en pour cent, il est indépendant du choix des unités de mesure permettant la comparaison des distributions de fréquence d’unité différente.
Exemple :
Le coefficient de variation des longueurs de la rectrice centrale des gélinottes huppées mâles juvéniles est égal à :
Quel est le coefficient de variation du nombre de galles par feuille pour la cécidomyie du hêtre ? Réponse.