Par définition, les variables aléatoires continues prennent des valeurs continues sur un intervalle donné.
La loi uniforme est la loi exacte de phénomènes continus uniformément répartis sur un intervalle.
La variable aléatoire X suit une loi uniforme sur le segment [a,b] avec a < b si sa densité de probabilité est donnée par :
f(x) = si x Î [a,b]
f(x) = 0 si x Ï [a,b]
Quelques commentaires :
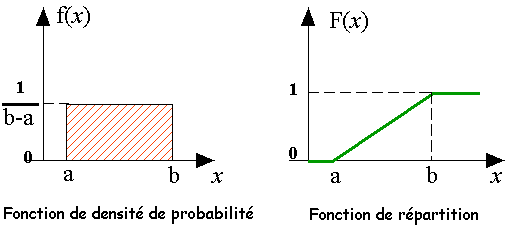
(1) La loi uniforme continue étant une loi de probabilité, l’aire hachurée en rouge sur la figure ci-dessus vaut 1. Ceci implique que la valeur prise par f(x) vaut .
(2) La probabilité que X Î [a’,b’] avec a’ < b’ et a’,b’ Î [a,b] vaut :
(3) La fonction de répartition associée à la loi uniforme continue est telle que :
FX (x) = 0 si x < a
FX (x) = 1 si x > b
FX (x) = si a £ x £ b
L’espérance de la loi uniforme continue vaut :
En effet par définition
cours analyse (Intégrale)
or et par définition de la loi uniforme continue
d’où
La variance de la loi uniforme continue vaut :
En effet par définition
même simplification que pour l’espérance
or et
d’où
On parle de loi normale lorsque l’on a affaire à une variable aléatoire continue dépendant d’un grand nombre de causes indépendantes dont les effets s’additionnent et dont aucune n’est prépondérante (conditions de Borel). Cette loi acquiert sa forme définitive avec Gauss (en 1809) et Laplace (en 1812). C’est pourquoi elle porte également les noms de : loi de Laplace, loi de Gauss et loi de Laplace-Gauss.
Exemple :
Ainsi la taille corporelle d’un animal dépend des facteurs environnementaux (disponibilité pour la nourriture, climat, prédation, etc.) et génétiques. Dans la mesure où ces facteurs sont indépendants et qu’aucun n’est prépondérant, on peut supposer que la taille corporelle suit une loi normale.
Une variable aléatoire absolument continue X suit une loi normale de paramètres (m , s) si sa densité de probabilité est donnée par :
: R ® R
avec m Î R et s Î R+
Notation : X ® N(m , s)
| Remarque : | On admet que =1 dans la mesure où l’intégration analytique est impossible. |
La fonction f est paire autour d’un axe de symétrie x = m car f(x + m ) = f(m - x)
d’où DE = [m , +¥[
La dérivé première f’’(x) est égale à : f’’(x) = f(x) Démonstration
d’où f ’(x) = 0 pour x = m et f ’(x) < 0 pour x > m
La dérivé seconde f ’’(x) est égale à : f ’’(x) = Démonstration
d’où f ’’(x) = 0 pour x = m + s et f ’’(x) > 0 pour x > m + s
|
|
m m + s + ∞ |
|
|
f ’’(x) |
- 0 + |
|
|
f ’(x) |
0 - |
|
|
f(x) |
0 |
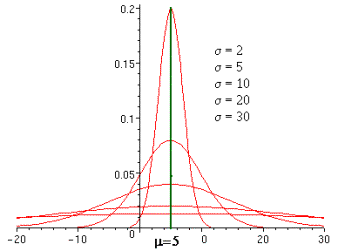
| Remarque : | Le paramètre m représente l’axe de symétrie et s le degré d’aplatissement de la courbe de la loi normale dont la forme est celle d’une courbe en cloche. |
L’espérance de la loi normale vaut :
E(X) = m
La variance de la loi normale vaut :
V(X) = s2
Théorème :
Soient X1 et X2 deux variables aléatoires normales indépendantes de paramètres
respectifs (m1, s1) , (m2, s2), alors leur somme X1+X2 est une variable aléatoire normale
de paramètres (m1 + m2, ).
(1) E(X1+X2) = E(X1 ) + E(X2) Propriété P1 de l’espérance.
or E(X1 ) = m1 et E(X2 ) = m2 d’où E(X1+X2) = m1 + m2
(2) V(X1+X2) =V(X1) + V(X2) Propriété P1 de la variance lorsque X1 et X2 sont indépendantes.
or V(X1) = s12 et V(X2) = s22 d’où V(X1+X2 ) = s12 + s22
Ce théorème se généralise immédiatement à la somme de n variables aléatoires normales indépendantes.
Une variable aléatoire continue X suit une loi normale réduite si sa densité de probabilité
est donnée par :
f : R ® R
| Remarque : | f est bien une loi de probabilité car : |
|
• " x ÎR, f(x) ³ 0 • f est intégrable sur ]-¥, + ¥[ et |
La fonction f est paire car f(-x) = f(x) d’où DE = [0,+¥ [
La dérivé première est f ’(x) = -x f(x) avec f ’(x) £ 0 pour x ≥ 0.
La dérivée seconde est f ’’(x) = -f(x) + x2f(x) = (x2 –1) f(x) qui s’annule pour x = 1 sur DE.
|
|
0 1 + ¥ |
|
|
f ’’(x) |
+ 0 - |
|
|
f ’(x) |
0 - |
|
|
f(x) |
0 |
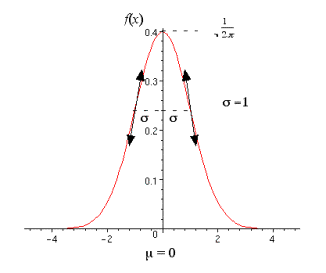
| Remarque : | L’axe de symétrie correspond à l’axe des ordonnées (x=0) et le degré d’aplatissement de la courbe de la loi normale réduite est 1. |
L’espérance d’une loi normale réduite est :
E(X) = 0
En effet par définition .
Or la fonction à intégrer est impaire d’où E(X)=0 (cours d’analyse : intégrale)
La variance d’une loi normale réduite est :
V(X) = 1
En effet par définition
d’où
En effectuant une intégration par partie :
avec = 0
or =1 par définition d’une fonction de répartition
d’où V(X) = 1
Si X suit une loi normale N (m,s), alors , une variable centrée réduite suit
une la loi normale réduite N (0,1).
La fonction de répartition de la loi normale réduite permet d’obtenir les probabilités associées à toutes variables aléatoires normales N(m,s) après transformation en variable centrée réduite.
On appelle fonction p , la fonction de répartition d’une variable normale réduite X
telle que : p : R ® R
Les propriétés associées à la fonction de répartition p sont :
(P1) p est croissante, continue et dérivable sur R et vérifie :
et
(P2) R p (t) + p (-t) = 1
R p (t) - p (-t) = 2p(t) - 1
Une application directe de la fonction est la lecture des probabilités sur la table de la loi normale réduite.
Exemple :
On suppose que la taille des individus suit une loi normale de paramètres (m,s). Sachant que 4% des individus mesurent moins de 160cm et 11% mesurent plus de 180cm, quelle est la valeur de m et s ? Réponse.
Définition
La loi de Pearson ou loi de (Khi deux) trouve de nombreuses applications dans le cadre de la comparaison de proportions, des tests de conformité d’une distribution observée à une distribution théorique et le test d’indépendance de deux caractères qualitatifs. Ce sont les test du khi-deux.
Soit X1, X2, …, Xi,…, Xn, n variables normales centrées réduites, on appelle
c2 la variable aléatoire définie par :
c2 = X12 + X22 +…+ Xi2 +…+ Xn2 =
On dit que c2 suit une loi de Pearson à n degrés de liberté (d.d.l.).
| Remarque : | Si n =1, la variable du c2 correspond au carré d’une variable normale réduite de loi N(0,1) |
|
(voir Rapport entre loi de probabilité). |
Propriétés :
(P1) Si X1, X2, X3, …, Xi,…, Xn sont n variables normales centrées réduites et s’il existe k relations de dépendance entre ces variables alors X12 + X22 + X32 +…+ Xi2 +…+ Xn2 suit une loi de Pearson à n - k degrés de liberté.
(P2) Si U suit une loi de Pearson à n d.d.l.,
si V suit une loi de Pearson à m d.d.l.,
et si U et V sont indépendantes alors U+ V suit une loi de Pearson à n+m ddl
U-V suit une loi de Pearson à n-m ddl (si n<m)
|
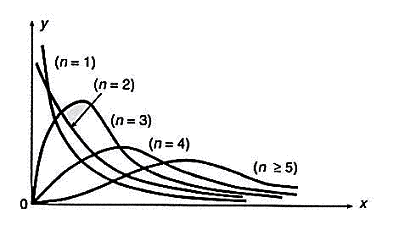
Pour c2 > 0, la fonction densité de probabilité est de la forme : avec Pour c2 £ 0 , f(c2) = 0 Pour n > 1, on utilise la table du Khi 2
|
|
| Remarque : | La constante est telle que . La distribution du c2 est dissymétrique et tend à devenir symétrique lorsque n augmente en se rapprochant de la distribution normale à laquelle elle peut être assimilée lorsque n > 30. |
L’espérance de la variable du c2 est :
E(c2) = n
car par définition E(c2) = avec Xi variable normale réduite
or V(Xi) = E(Xi 2) - E(Xi)2 = 1 pour la variable normale réduite avec E(Xi) = 0
d’où E(Xi 2) = 1 et donc E(c2) = n
La variance de la variable du c2 est :
V(c2) = 2n
car par définition les Xi variables normales réduites étant indépendantes,
V(c2) = et d’autre part V(Xi2) = E(Xi 4) – [E(Xi2)]2
or E(Xi 4) = 3 d’où V(Xi2) = 3 – 1 = 2
ainsi V(c2) = = 2n
La loi de Student (ou loi de Student-Fisher) est utilisée lors des tests de comparaison de paramètres comme la moyenne et dans l’estimation de paramètres de la population à partir de données sur une échantillon (Test de Student). Student est le pseudonyme du statisticien anglais William Gosset qui travaillait comme conseiller à la brasserie Guinness et qui publia en 1908 sous ce nom, une étude portant sur cette variable aléatoire.
Soit U une variable aléatoire suivant une loi normale réduite N(0,1) et V une variable aléatoire suivant une loi de Pearson à n degrés de liberté cn2 , U et V étant indépendantes, on dit alors que suit une loi de Student à n degrés de liberté.
|
La fonction densité de probabilité est de la forme :
Calcul des probabilités avec la table de la loi de Student
|
|
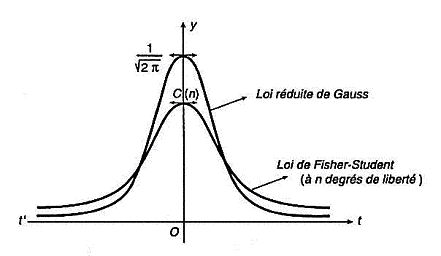
| Remarque : | La constante est telle que . La distribution du T de Student est symétrique et tend vers une loi normale lorsque n augmente indéfiniment. |
L’espérance de la variable de Student est :
si n >1
La variance de la variable de Student est :
si n > 2
La loi de Fisher-Snedecor est utilisée pour comparer deux variances observées et sert surtout dans les très nombreux tests d’analyse de variance et de covariance.
Soit U et V deux variables aléatoires indépendantes suivant une loi de Pearson respectivement à n et m degrés de liberté.
On dit que suit une loi de Fisher-Snedecor à degrés de liberté.
|
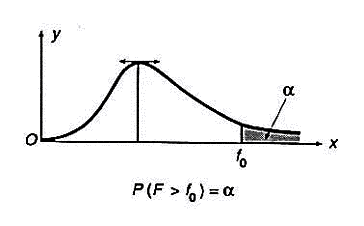
Pour F > 0, la fonction densité de probabilité est de la forme :
Pour F £ 0, f(F) = 0 Utilisation des tables de Fisher-Snedecor pour le calcul des probabilités.
|
|
| Remarque : | Si n = 1, alors on a la relation suivante : (voir Rapport entre loi de probabilité). |
L’espérance de la variable de Fisher-Snédecor est :
si m >2
La variance de la variable de Fisher-Snédecor est :
si m > 4
