Chapitre 6 : Estimation

3 Estimateur

3.1 Définition

Soient X₁, X₂,…, X_i, ..., X_n_,n réalisations indépendantes de la variable aléatoire X (discrète ou continue) et q un paramètre associé à la loi de probabilité suivi par X, un estimateur du paramètre q est une variable aléatoire Q fonction des X_i_:

Q = f (X₁, X₂,…, X_i, ..., X_n)

Si on considère n observations x₁, x₂,…, x_i, ..., x_n, l’estimateur Qfournira une estimation de q notée également :

= f (x₁, x₂,…, x_i, ..., x_n)

L'estimation d'un paramètre inconnu, noté q est fonction des observations résultant d'un échantillonnage aléatoire simple de la population. L’estimateur est donc une nouvelle variable aléatoire construite à partir des données expérimentales et dont la valeur se rapproche du paramètre que l’on cherche à connaître.

L'estimation de q est une variable aléatoire Q dont la distribution de probabilité s'appelle

la distribution d'échantillonnage du paramètre q. L'estimateur Q admet donc une

espérance E(Q) et une variance V(Q).

3.2 Propriétés

3.2.1 Convergence

L’estimateur Q doit tendre vers la valeur réelle du paramètre q lorsque le nombre

d'individus étudié augmente. On dit que l'estimateur est convergent.

si "e > 0 P(½Q - q½) > e) ® 0 lorsque n ® ¥

Ceci équivaut à dire qu’en limite Q ® q lorsque n ® ¥.

3.2.2 Biais d’un estimateur

Le biais d’un estimateur noté B(Q) est la différence moyenne entre sa valeur et celle du paramètre qu’il estime. Le biais doit être égal à 0 pour avoir un bon estimateur.

B(Q) = E(Q-q) = E(Q)-E(q) = E(Q)-q = 0 (voir propriétés de l’espérance)

d’où E(Q) = q

Exemple :

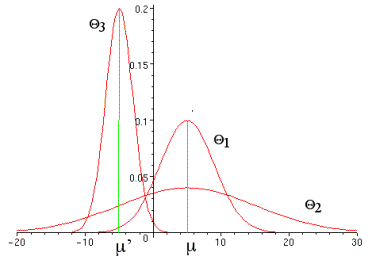
Soit les densités de probabilité de 3 estimateurs d’une espérance m,

Q₁ et Q₂ sont des estimateurs sans biais de m car E(Q₁) = E(Q₂) = m

Q₃ est un estimateur biaisé de m car

E(Q₃) - m = m’- m ¹ 0

Dans l’exemple ci-dessus, Q₁ et Q₂ sont des estimateurs sans biais de m car

B(Q₁) = E(Q₁- m ) = E(Q₁)- m = 0 car E(Q₁) = m , de même pour B(Q₂)

alors que Q₃est un estimateur biaisé de m car

B(Q₃) = E(Q₃- m ) = E(Q₃)- m = m’ - m ¹ 0 car E(Q₃) = m’

Remarque :	Un estimateur est asymptotiquement sans biais si E(Q) ® q lorsque n ® ∞

3.2.3 Variance d’un estimateur

Si deux estimateurs sont convergents et sans biais, le plus efficace est celui qui a la variance la plus faible car ses valeurs sont en moyenne plus proches de la quantité estimée.

V(Q) = E(Q - E(Q))²minimale

Exemple

Dans l’exemple précédent, on voit que V(Q₁) < V(Q₂). On peut donc conclure que Q₁est un meilleur estimateur de m que Q₂.

Remarque :	Quand les estimateurs sont biaisés, en revanche, leur comparaison n’est pas simple.
	Ainsi un estimateur peu biaisé mais de variance très faible, pourrait même être préféré à un estimateur sans biais mais de grande variance

Théorème :

Si un estimateur est asymptotiquement sans biais et si sa variance tend vers 0 lorsque n ® ¥, il est convergent.

P(½Q- q ½ ³ e ) £ avec e > 0

(Inégalité de Bienaymé-Tchébycheff)