Chapitre 6 : Estimation
4
Estimation ponctuelle et par intervalle
L’estimation d’un paramètre quelconque q est ponctuelle si l’on associe une seule valeur à l’estimateur à partir des données observables sur un
échantillon aléatoire. L’estimation par intervalle associe à un
échantillon aléatoire, un intervalle [ ] qui recouvre q avec
une certaine probabilité.
4.1.
Estimation ponctuelle
Si la distribution de la variable aléatoire X est connue, on utilise la méthode du maximum
de vraisemblance pour estimer
les paramètres de la loi de probabilité. En revanche si la distribution n'est
pas connue, on utilise la méthode des moindres carrés.
4.1.1.
Espérance
Soit X une
variable aléatoire continue suivant une loi normale N(m,s)
dont la valeur des paramètres n’est pas connue et pour laquelle on souhaite
estimer
l’espérance m.
Soient X1 , X2 ,…, Xi ,
..., Xn , n réalisations indépendantes de
la variable aléatoire X, un
estimateur du paramètre m est une suite de variable
aléatoire Q fonctions des Xi :
Q = f (X1 , X2 ,…, Xi , ..., Xn)
La méthode des moindres carrés consiste à rechercher les
coefficients de la combinaison linéaire Q
= a1X1 + a2X2 +…+ aiXi
+ ...+ anXn
telle que E (Q) = m et V(Q) soit minimale
La moyenne arithmétique constitue le meilleur
estimateur de m, espérance
de
la loi de probabilité de la variable aléatoire X :
Voici pourquoi :
Estimateur sans biais : E(
) = m (voir loi de la
moyenne)
Estimateur convergent : si l’on pose l’inégalité de Biénaymé-Tchébycheff :
P(½
- m ½ ³ e ) £
avec
e > 0
lorsque n ®¥
=
® 0 et ceci "e > 0
ainsi en limite, P(½
- m ½ ³ e ) = 0, ce qui indique que
® m en
probabilité.
4.1.2.
Variance
Soit X une variable
aléatoire continue suivant une loi normale N (m,s) pour
laquelle on souhaite estimer la variance s2.
Soient X1 , X2 ,…, Xi ,
..., Xn , n réalisations indépendantes de
la variable aléatoire X, un
estimateur du paramètre s2 est une suite de variable
aléatoire Q fonctions des Xi :
Q = f (X1 , X2 ,…, Xi , ..., Xn)
· Cas où l’espérance m
est connue
La méthode des moindres carrés consiste à rechercher les
coefficients de la combinaison linéaire
Q = a1(X1 - m)2 + a2(X2 - m)2
+…+ ai(Xi-
m)2 +...+ an
( Xn-
m)2
telle que E (Q) = s2 et V(Q) soit minimale (voir démonstration)
La variance observée constitue le meilleur
estimateur de s2, variance de la loi de
probabilité de la variable aléatoire X lorsque m est connue:
| Remarque : |
Cette estimation de la variance de la population est
rarement utilisée dans la mesure où si la variance s2 n’est pas connue, l’espérance m ne l’est pas non plus. |
|
|
· Cas où l’espérance m
est inconnue
Dans ce cas, nous allons estimer m avec
et dans ce cas
.
Nous allons étudier la relation entre ces deux termes à partir de la variance
observée :
avec
=
en effet
ainsi
Le meilleur estimateur de s2, variance
de la loi de probabilité de la variable aléatoire
X lorsque l’espérance m est inconnue est :
| Remarque : |
Lorsque n
augmente, la variance observée s2 tend vers la variance de la
population s2.
|
|
|
4.1.3.
Fréquence
Soit le schéma de Bernoulli dans lequel le caractère A
correspond au succès. On note p la
fréquence des individus de la population possédant le caractère A. La valeur
de ce paramètre étant inconnu, on cherche à estimer la fréquence p à partir des données observables sur
un échantillon.
A chaque échantillon non exhaustif de taille n, on associe l’entier k, nombre d’individus possédant le
caractère A.
Soit K une
variable aléatoire discrète suivant une loi binomiale B(n,p) et pour laquelle on souhaite estimer la fréquence p.
La fréquence observée du
nombre de succès observé dans un échantillon de taille n
constitue le meilleur estimateur de p:
Voici pourquoi :
Estimateur sans biais : E(
) = p (voir loi de fréquence)
Estimateur convergent : si l’on pose l’inégalité de
Biénaymé-Tchébycheff
P(½
- p ½
³ e ) £
avec
e > 0
alors lorsque n ® ¥
® 0 et ceci "e > 0
ainsi en limite P(½
- p½³ e ) = 0 ce qui
indique que
® p en probabilité.
Exemple :
On a prélevé au hasard, dans une population de lapin, 100
individus. Sur ces 100 lapins, 20 sont atteints par la myxomatose. Le
pourcentage de lapins atteints par la myxomatose dans la population est
donc :
=
= 0,2 soit 20% de lapins atteins dans la population
Ce résultat n’aura de signification que s’il est associé à un intervalle de confiance.
4.2.
Estimation par intervalle
4.2.1.
Définition
L’estimation par intervalle associe à un
échantillon aléatoire, un intervalle [
] qui recouvre q avec
une certaine probabilité.
Cet intervalle est appelé l’intervalle
de confiance du paramètre q car
la probabilité que
q dont la valeur est inconnue se trouve compris entre
est égale à 1-a, le coefficient
de confiance P(
< q <
) = 1 - a
Son complément a correspond au coefficient de risque.
P(q ¹ [
,
] ) = a
Un intervalle de confiance indique la précision d’une estimation car
pour un risque a donné, l’intervalle
est d’autant plus grand que la précision est faible comme l’indiquent les
graphes ci-dessous. Pour chaque graphe,
l’aire hachurée en vert correspond au
coefficient de risque a. Ainsi
de part et d’autre de la distribution,
la valeur de l’aire hachurée vaut
.
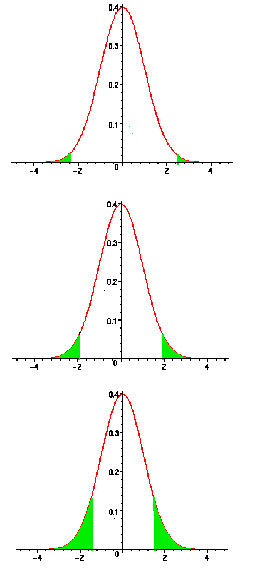 |
a = 0,01
99 chances sur 100 que la valeur du paramètre recherché se trouve dans l’intervalle de confiance mais la précision autour de la valeur prédite est faible
|
|
a = 0,05
95 chances sur 100 que la valeur du paramètre recherché se trouve dans l’intervalle de confiance et la précision autour de la valeur prédite est correcte.
|
|
a =
0,10
90 chances sur 100 que la valeur du paramètre
recherché se trouve dans l’intervalle de confiance mais la précision
autour de la valeur prédite est élevée.
|
4.1.2
Intervalle de confiance d’une moyenne
En fonction de la nature de la variable aléatoire continue X, de la taille de l’échantillon n et de la connaissance que nous avons
sur le paramètre s2,
l’établissement de l’intervalle de confiance autour
de m sera différent.
· Quelque soit la valeur de n, si X ® N(m , s ) et la variance s2 est connue,
Etablir l’intervalle de confiance autour de la moyenne m revient à établir la valeur de i pour
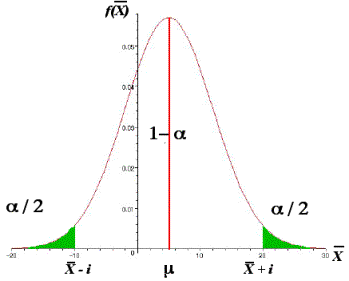
une valeur du coefficient de confiance 1 - a donnée par l’expérimentateur.
Voici pourquoi :
Si P(
- i < m <
+ i ) = 1 - a alors
P(m - i
<
< m + i ) = 1 - a
Connaissant la loi
suivie par la
v. a.
et d’après le théorème central limite, nous pouvons établir que
sachant que
N(0,1) (conditions)
par conséquent
correspond à la valeur de la variable normale
réduite pour la probabilité a donnée
notée ea ou écart réduit
ainsi
= ea implique
L’intervalle de
confiance de la moyenne m pour un coefficient de
risque a est donc
quelque soit la valeur de n si X ® N(m , s ) et la variance s2 est connue
Exemple :
Pour des masses comprises entre
50g et 200g, une balance donne une pesée avec une variance de 0,0015. Les
résultats des trois pesées d’un même corps sont : 64,32 ;
64,27 ; 64 ,39.
On veut connaître le poids moyen
de ce corps dans la population avec un coefficient de confiance de 99%.
avec
= 64,33g et
ea = 2,576 alors
=
= 0,058
et donc
= 64,33g ± 0,058
d’où le poids moyen de ce corps est compris dans
l’intervalle [64,27 ; 64,39] avec une probabilité de 0,99.
| Remarque : |
La valeur de ea est donnée par la table de l’écart-réduit pour une valeur a donnée. |
|
|
Coefficient de risque
|
Ecart-réduit
|
|
a = 0,01
|
ea = 2,576
|
|
a = 0,05
|
ea = 1,960
|
|
a = 0,10
|
ea = 1,645
|
|
· Quelque soit la valeur de n, si X ® N(m , s ) et la variance s2 est inconnue,
Le raisonnement reste le même mais la variance de la
population s2 doit
être estimée par
(voir estimation ponctuelle)
Si P(
- i < m <
+ i ) = 1 - a alors
P(m - i
<
< m + i ) = 1 - a
Connaissant la loi
suivie par la v. a.
et celle suivie par la variable centrée
réduite, on peut établir que
sachant que
T(n-1 d.d.l.) (conditions)
par conséquent
correspond à la valeur de la variable de
student pour une valeur de probabilité a donnée notée ta pour n -1 degrés de liberté.
Ainsi
= ta implique i = ta x
L’intervalle de confiance de l’espérance m pour un coefficient de risque a est donc
quelque soit la valeur de n si X ® N(m , s) et la variance s2 est inconnue
| Remarque : |
Lorsque n > 30, la loi de student converge vers une
loi normale réduite. Ainsi la valeur de ta (n-1) est égale à ea |
|
Ci-dessous, un exemple pour un risque a = 0,05
|
Taille de l’échantillon
|
Ecart-réduit
|
Variable de student
|
|
n = 10
|
ea = 1,960
|
ta
= 2,228
|
|
n = 20
|
ea = 1,960
|
ta
= 2,086
|
|
n = 30
|
ea = 1,960
|
ta
= 2,042
|
|
n = 40
|
ea = 1,960
|
ta
= 1,960
|
|
Exemples :
(1) Dans un échantillon de 20 étudiants
de même classe d’âge et de même sexe, la taille moyenne observée est de 1,73m
et l’écart-type de 10 cm. La taille moyenne de l’ensemble des étudiants de
l’université est donc :
avec
= 1,73m ;
=
= 0,011
et ta
= 2,086
d’où
=
= 0,049 ainsi
= 1,73m ± 0,049
La taille moyenne des étudiants dans la population
est comprise dans l’intervalle [1,68 ; 1,78] avec
une probabilité de 0,95.
(2) Dans un échantillon de 100
étudiants, la taille moyenne de la population est :
= 1,73m ;
=
= 0,01
et ea = 1,960
d’où
=
= 0,02 ainsi
= 1,73m ± 0,02
La taille moyenne des étudiants dans la population
est comprise dans l’intervalle [1,71 ; 1,75] avec
une probabilité de 0,95.
Ainsi lorsque la taille de l’échantillon augmente pour un même coefficient de
confiance
(1-a) ,
l’estimation autour de m est
plus précise.
· Si n > 30 et X suit une loi inconnue,
La démarche est la même que pour le cas précédent puisque
par définition la variance de la population est inconnue et doit être estimée
avec la variance observée :
(voir estimation
ponctuelle)
Comme pour le cas 1, la loi suivie par la variable centrée
réduite
N(0,1) (conditions).
L’intervalle de confiance de l’espérance m pour un coefficient de
risque a est donc
vraie seulement si n est grand.
· Si n < 30 et X suit une loi inconnue,
La loi de probabilité suivie par
n’est pas connue et l’on a recours aux statistiques non paramétriques.
4.1.3 Intervalle de confiance d’une proportion
Etablir l’intervalle de confiance autour de la fréquence p de la population à partir de son estimateur
revient à établir la valeur de i pour une valeur du coefficient de confiance
(1 - a) donnée par l’expérimentateur telle que :
P(
- i < p <
+ i ) = 1 - a ou P(p - i <
< p + i ) = 1 - a
Connaissant la loi suivie par la v. a.
et d’après le théorème central limite, on peut
établir que
sachant que
N(0,1)
par conséquent
correspond à la valeur de la variable normale réduite pour la probabilité a donnée notée ea ou écart réduit.
ainsi
= ea implique
Par définition, V(
) =
n’est pas connue et on l’estime par
avec
et
L’intervalle de confiance de la fréquence p pour un coefficient de risque a est donc
vraie seulement si n est grand et np, nq > 5
| Remarque : |
Si la taille de l’échantillon est faible, on a recours aux lois exactes. |
|
|
Exemple :
Un laboratoire d’agronomie a effectué une étude sur le maintien du pouvoir germinatif des graines de Papivorus subquaticus après une conservation de 3 ans.
Sur un lot de 80 graines, 47 ont germé. Ainsi la probabilité de germination des graines de Papivorus subquaticus après trois ans de conservation avec un coefficient de confiance de 95% est donc :
avec
=
= 0,588 ,
=
= 0,412 et ea = 1,96
alors
=
= 0,108 d’où p = 0,588 ± 0,108
ainsi la probabilité de germination est comprise dans l’intervalle [0,480 et 0,696] avec une probabilité de 0,95.

