Chapitre 6 : Estimation

2         Distribution d’échantillonnage

Pour résoudre les problèmes d’estimation de paramètres inconnus, il faut tout d’abord étudier les distributions d’échantillonnage, c’est à dire la loi de probabilité suivie par l’estimateur.

 

Remarque :

En théorie de l’estimation, il s’agit de distinguer soigneusement trois concepts différents :

- les paramètres de la population comme la moyenne m dont la valeur est certaine mais inconnue symbolisés par des lettres grecques. -  les résultats de l’échantillonnage comme la moyenne  dont la valeur est certaine mais connue symbolisés par des minuscules. - les variables aléatoires des paramètres, comme la moyenne aléatoire  dont la valeur est incertaine puisque aléatoire mais dont la loi de probabilité est souvent connue et symbolisées par des majuscules.

 

2.1     Définition

2.1.1                    Approche empirique

 

Il est possible d’extraire d’une population de paramètres  p, m ou s² pour une variable aléatoire X, k échantillons aléatoires simples de même effectif, n. Sur chaque échantillon de taille n, on calcule les paramètres descriptifs (f, , s²).

                    

 

 

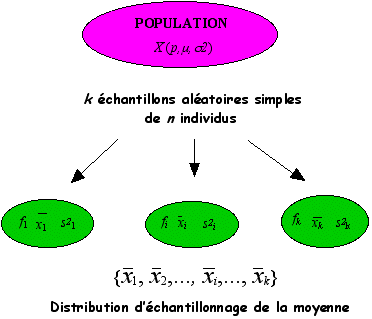
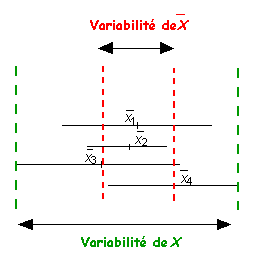
On obtient ainsi pour chaque paramètre estimé, une série statistique composée de k éléments à savoir les k estimations du paramètre étudié. Par exemple, on aura k valeurs de moyennes observées  (graphe ci-dessus).

 

La distribution associée à ces k estimations constitue la distribution d’échantillonnage du paramètre. On peut alors associer une variable aléatoire à chacun des paramètres. La loi de probabilité suivie par cette variable aléatoire admet comme distribution, la distribution d’échantillonnage du paramètre auquel on pourra associer une espérance et une variance.

 

2.1.2                   Approche théorique

En pratique, les données étudiées sont relatives à un seul échantillon. C’est pourquoi, il faut rechercher les propriétés des échantillons susceptibles d’être prélevés de la population ou plus précisément les lois de probabilité de variables aléatoires associées à un échantillon aléatoire.

 

 

 

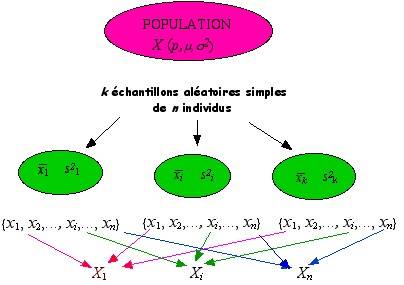
Ainsi les n observations x₁ , x₂ ,…, x_i , ..., x_n, faites sur un échantillon peuvent être considérées comme n variables aléatoires X₁ , X₂ ,…, X_i , ..., X_n. En effet, la valeur prise par le premier élément extrait de la population X₁, dépend de l’échantillon obtenu lors du tirage aléatoire. Cette valeur sera différente si l’on considère un autre échantillon. Il en est de même pour les n valeurs extraites de la population.

 

A partir de ces n variables aléatoires, on peut définir alors une nouvelle variable qui sera fonction de ces dernières telle que :

                                   Y = f(X₁, X₂,…, X_i , ..., X_n )

par exemple :  Y = X₁ + X₂+…+ X_i +. …X_n

 

Ainsi la loi de probabilité de la variable aléatoire Y dépendra à la fois de la loi de probabilité de la variable aléatoire X   et de la nature de la fonction f.

 

2.2       Loi de probabilité de la moyenne

2.2.1                   Définition

Soit X une variable aléatoire suivant une loi normale d’espérance m et de variance s²  et

 n copies indépendantes X₁,X₂,…,X_i,…,X_n telle que X_i associe le i^ème élément de chacun des n échantillons avec E(X_i) = m et V(X_i) = s².

 

On construit alors la variable aléatoire , telle que

   

avec pour espérance :

         Propriétés de l’espérance

 

et pour variance si V(X_i) = s²:

    Propriétés de la variance

 

 

Remarque :	il est aisé de voir sur le graphe ci-dessous que la variance associée à une moyenne (  ) est plus faible que la variance de la variable elle-même (s2).

 

Soit l’étendue des valeurs observées d’une variable aléatoire X pour 4 échantillons de même taille issus d’une même population.   Les valeurs des moyennes arithmétiques sont indiquées ainsi que les limites relatives à l’étendue des valeurs de la variable observée et celle des moyennes observées.

 

 

Exemple : 

Des études statistiques montrent que le taux de glucose dans le sang est une variable normale X  d’espérance m = 1 g/l et d’écart-type s = 0,1 g/l.

En prenant un échantillon de 9 individus dans la population, l’espérance et l’écart-type théorique attendu de la variable aléatoire  sont alors :

             = m = 1 g/l  et     =  =  = 0,03 g/l

 

2.2.2                 Convergence

En fonction de la nature de la variable aléatoire continue X, de la taille de l’échantillon n et de la connaissance que nous avons sur le paramètre s², la variable centrée réduite construite avec  converge vers différentes lois de probabilité (Table de convergence).

 

Ceci reste vrai lorsque  n £ 30 seulement si la loi suivie par X suit une loi normale.

 

 

 

2.3       Loi de probabilité d’une fréquence

Soit une population dans laquelle une proportion p des individus présente une certaine propriété.

Si k est le nombre d’individu présentant la propriété dans un échantillon de taille n, alors la variable aléatoire K résultant de différents échantillonnages suit une loi binomiale B(n,p) avec E(K) = np et V(K) = npq.

 

On construit la variable aléatoire       avec

pour espérance :           Opération sur les variables

et pour  variance :