Le principe des tests d’hypothèse est de poser une hypothèse de travail et de prédire les conséquences de cette hypothèse pour la population ou l’échantillon. On compare ces prédictions avec les observations et l’on conclut en acceptant ou en rejetant l’hypothèse de travail à partir de règles de décisions objectives.
Définir les hypothèses de travail, constitue un élément essentiel des tests d'hypothèses de même que vérifier les conditions d'application de ces dernières (normalité de la variable, égalité des variances ou homoscédasticité, etc).
Différentes étapes doivent être suivies pour tester une hypothèse :
(1) définir l’hypothèse nulle (notée H0) à contrôler,
(2) choisir un test statistique ou une statistique pour contrôler H0,
(3) définir la distribution de la statistique sous l’hypothèse « H0 est réalisée »,
(4) définir le niveau de signification du test ou région critique notée a,
(5) calculer, à partir des données fournies par l’échantillon, la valeur de la statistique
(6) prendre une décision concernant l’hypothèse posée et faire une interprétation biologique
L’hypothèse nulle notée H0 est l’hypothèse que l’on désire contrôler : elle consiste à dire qu’il n’existe pas de différence entre les paramètres comparés ou que la différence observée n’est pas significative et est due aux fluctuations d’échantillonnage.
Cette hypothèse est formulée dans le but d’être rejetée.
Exemple :
|
Tabac |
Si l’on désire comparer la fréquence de fumeurs dans la population estudiantine (notée p) à la fréquence de fumeurs dans la population en général (notée p0), l’hypothèse nulle testée est la suivante : H0 : p = p0 (test de conformité) |
La différence de fréquence des fumeurs n’est pas significativement différente entre les deux populations comparées.
L’hypothèse alternative notée H1 est la négation de H0, elle est équivalente à dire « H0 est fausse ». La décision de rejeter H0 signifie que H1 est réalisée ou H1 est vraie.
| Remarque : | Il existe une dissymétrie importante dans les conclusions des tests. En effet, la décision d’accepter H0 n’est pas équivalente à « H0 est vraie et H1 est fausse ». |
|
Cela traduit seulement l’opinion selon laquelle, il n’y a pas d’évidence nette pour que
H0 soit fausse.
Un test conduit à rejeter ou à ne pas rejeter une hypothèse nulle jamais à l’accepter d’emblée. |
La nature de H0 détermine la façon de formuler H1 et par conséquence la nature unilatérale ou bilatérale du test.
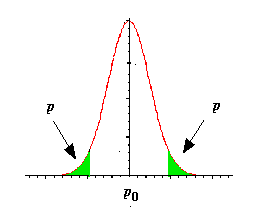
Test bilatéral
Si H0 consiste à dire que la population estudiantine avec la fréquence de fumeurs p est représentative de la population avec la fréquence de fumeurs p0, on pose alors :
H0 : p = p0 et H1 : p ¹ p0
|
|
H0 : p = p0 et H1 : p ¹ p0 Le test sera bilatéral car on considère que la fréquence p peut être supérieure ou inférieure à la fréquence p0 . La région critique a en vert correspond à une probabilité a/2 de part et d’autre de la courbe. |
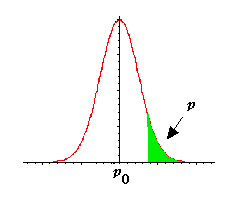
Test unilatéral
Si l’on fait l’hypothèse que la fréquence de fumeurs dans la population estudiantine p est supérieure à la fréquence de fumeurs dans la population p0, on pose alors
H0 : p = p0 et H1 : p > p0
:
|
|
H0 : p = p0 et H1 : p > p0 Le test sera unilatéral car on considère que la fréquence p ne peut être que supérieure à la fréquence p0 . La région critique a en vert correspond à une probabilité a. |
Le raisonnement inverse peut être formulé avec l’hypothèse suivante :
H0 : p = p0 et H1 : p < p0
| Remarque : | Seuls les tests bilatéraux seront développés dans le cours. Les tests unilatéraux seront traités au niveau des exemples. |
Ce choix dépend de la nature des données, du type d’hypothèse que l’on désire contrôler, des affirmations que l’on peut admettre concernant la nature des populations étudiées (normalité, égalité des variances) et d’autres critères que nous préciserons.
Un test statistique ou une statistique est une fonction des variables aléatoires représentant l’échantillon dont la valeur numérique obtenue pour l’échantillon considéré permet de distinguer entre H0 vraie et H0 fausse.
Dans la mesure où la loi de probabilité suivie par le paramètre p0 au niveau de la population en général est connue, on peut ainsi établir la loi de probabilité de la statistique S telle que :
S = p – p0 (voir Intervalle de confiance d’une fréquence)
Connaissant la loi de probabilité suivie par la statistique S sous l’hypothèse H0 , il est possible d’établir une valeur seuil, Sseuil de la statistique pour une probabilité donnée appelée le niveau de signification du test : a.
La région critique correspond à l’ensemble des valeurs telles que
S > Sseuil
et le niveau de signification est telle que :
P(S > Sseuil) = a avec P(S £ Sseuil) = 1 - a
Selon la nature unilatérale ou bilatérale du test, la définition de la région critique varie.
|
|
Test unilatéral H0 : p = p0 |
Test bilatéral H0 : p = p0 |
|
|
Hypothèse alternative |
H1 : p > p0 |
H1 : p < p0 |
H1 : p ¹ p0 |
|
Valeur de S sous H1 S = p – p0 |
S > 0 |
S < 0 |
½S ½¹ 0 |
|
Niveau de signification a |
P(S > Sseuil) = a |
P(S < Sseuil) = a |
P(½S½> Sseuil) = a |
Il existe deux stratégies pour prendre une décision en ce qui concerne un test d’hypothèse :
la première stratégie fixe a priori la valeur du seuil de signification a et la seconde établit la valeur de la probabilité critique aobs a posteriori.
Règles de décision 1 :
Sous l’hypothèse « H0 est vraie » et pour un seuil de signification a fixé
· si la valeur de la statistique S calculée (Sobs.) est supérieure à la valeur seuil Sseuil
Sobs > Sseuil alors l’hypothèse H0 est rejetée au risque d’erreur a
et l’hypothèse H1 est acceptée.
· si la valeur de la statistique S calculée (Sobs.) est inférieure à la valeur seuil Sseuil
Sobs £ Sseuil alors l’hypothèse H0 ne peut être rejetée.
| Remarque : | Le choix du risque a est lié aux conséquences pratiques de la décision : |
|
si les conséquences sont graves, on choisira a = 1% ou 1‰, mais si le débat est plutôt académique, le traditionnel a = 5 % fera le plus souvent l’affaire. |
Règles de décision 2 :
La probabilité critique a telle que P(S ³ Sobs.) = aobs est évaluée
· si aobs ³ 0,05 l’hypothèse H0 est acceptée car le risque d’erreur de rejeter H0 alors qu’elle est vrai est trop important.
· si aobs < 0,05 l’hypothèse H0 est rejetée car le risque d’erreur de rejeter H0 alors qu’elle est vrai est très faible.
Le risque d’erreur a est la probabilité que la valeur expérimentale ou calculée de la statistique S appartienne à la région critique si H0 est vrai. Dans ce cas H0 est rejetée et H1 est considérée comme vraie.
Le risque a de première espèce est celui de rejeter H0 alors qu'elle est vraie
a = P( rejeter H0 / H0 vraie)
ou accepter H1 alors qu’elle est fausse
a = P( accepter H1 / H1 fausse)
La valeur du risque a doit être fixée a priori par l’expérimentateur et jamais en fonction des données. C’est un compromis entre le risque de conclure à tort et la faculté de conclure.
| Remarque : | Toutes choses étant égales par ailleurs, la région critique diminue lorsque a décroît (voir intervalle de confiance) et donc on rejette moins fréquemment H0. |
|
A vouloir commettre moins d’erreurs, on conclut plus rarement. |
Exemple :
Si l’on cherche à tester l’hypothèse qu’une pièce de monnaie n’est pas « truquée », nous allons adopter la régle de décision suivante :
|
|
H0 : la pièce n’est pas truquée est acceptée si X Î [40,60] rejetée si X Ï [40,60] donc soit X < 40 ou X > 60 |
avec X « nombre de faces » obtenues en lançant 100 fois la pièce.
Quel est le risque d’erreur de première espèce a dans ce cas ? Réponse.
Le risque d’erreur b est la probabilité que la valeur expérimentale ou calculée de la statistique n’appartienne pas à la région critique si H1 est vrai. Dans ce cas H0 est acceptée et H1 est considérée comme fausse.
Le risque b de deuxième espèce est celui d’accepter H0 alors qu'elle est fausse
b = P( accepter H0 / H0 fausse) ou P( accepter H0 / H1 vraie)
ou rejeter H1 alors qu’elle est vraie
b = P( rejeter H1 / H1 vraie)
| Remarque : | Pour quantifier le risque b, il faut connaître la loi de probabilité de la statistique S sous l’hypothèse H1. |
Exemple :
Si l’on reprend l’exemple précédent de la pièce de monnaie, la probabilité p d’obtenir face est de 0,6 pour une pièce truquée. Si l’on adopte toujours la même régle de décision :
|
|
H0 : la pièce n’est pas truquée est acceptée si X Î [40,60] rejetée si X Ï [40,60] donc soit X < 40 ou X > 60 |
avec X « nombre de faces » obtenues en lançant 100 fois la pièce.
Quel est le risque d’erreur de second espèce b dans ce cas ? Réponse.
Les tests ne sont pas faits pour « démontrer » H0 mais pour « rejeter » H0 . L’aptitude d’un test à rejeter H0 alors qu’elle est fausse constitue la puissance du test.
La puissance d’un test est : 1 - b = P( rejeter H0 / H0 fausse) = P(accepter H1/H1 vraie)
La relation entre les deux risques d’erreur figure sur le graphe ci-dessous.
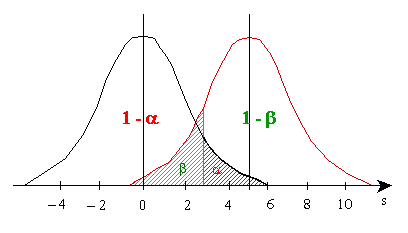
La puissance d’un test est fonction de la nature de H1, un test unilatéral est plus puissant qu'un test bilatéral.
La puissance d’un test augmente avec taille de l'échantillon N étudié à valeur de a constant.
La puissance d’un test diminue lorsque a diminue.
Exemple :
Si l’on reprend l’exemple précédent de la
, calculez la puissance du test lorsque
la probabilité d’obtenir face est respectivement 0,3 - 0,4 - 0,6 - 0,7 -0,8 pour une pièce truquée. Que constatez-vous ? Réponse.
Les différentes situations que l’on peut rencontrer dans le cadre des tests d’hypothèse sont résumées dans le tableau suivant :
|
Réalité Décision |
H0 vraie |
H0 fausse |
|
Non-rejet de H0 |
correct |
Manque de puissance risque de second espèce b |
|
Rejet de H0 |
Rejet à tort risque de première espèce a |
Puissance du test 1 - b |
La robustesse d’un test statistique représente sa sensibilité à des écarts aux
hypothèses faites.
Exemple : Toute chose étant égale par ailleurs, que se passe-t-il si l’hypothèse de normalité n’est pas satistfaite ?
