Chapitre 7 : Test d’hypothèse

3         Tests de conformité

Les tests de conformité sont destinés à vérifier si un échantillon peut être considéré comme extrait d’une population donnée ou représentatif de cette population, vis-à-vis d'un paramètre comme la moyenne, la variance ou la fréquence observée. Ceci implique que la loi théorique du paramètre est connue au niveau de la population.

 

En théorie, si l’on suppose connu la valeur q₀ d’un paramètre relatif à la population

(par exemple p, m , s² ) et  un estimateur absolument correct de q (par exemple , , s²) obtenu à partir d’un échantillon aléatoire simple de taille n, on cherche à savoir si l’échantillon est représentatif de la population pour le paramètre considéré.

                                H₀ :  q = q₀  (test de conformité)

 

3.1     Comparaison d’une moyenne observée et d’une moyenne théorique

3.1.1   Principe du test

Soit X, une variable aléatoire observée sur une population, suivant une loi normale et un échantillon extrait de cette population.

 

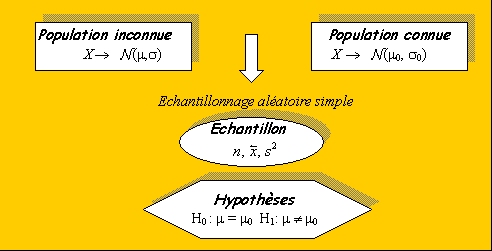
Le but est de savoir si un échantillon de moyenne , estimateur de m, appartient à une population de référence connue d’espérance m₀ (H₀ vraie) et ne diffère de m₀ que par des fluctuations d’échantillonnage ou bien appartient à une autre population inconnue d’espérance m (H₁ vraie).

 

Pour tester cette hypothèse, il existe deux statistiques : la variance  de la population de référence est connue (test e) ou cette variance est inconnue et il faut l’estimer (test T).

 

3.1.2  Variance de la population connue

 

3.1.2.1           Statistique du test

 Soit  la distribution d’échantillonnage de la moyenne dans la population inconnue  suit une loi normale telle que :   ®  N (m,  ).  

La statistique étudiée est l’écart : S =  - m₀  dont la distribution de probabilité est la suivante

    S ® N (0,  )     avec    sous H₀,  E(S) = 0  et   V(S) =     (voir démonstration)

Nous pouvons établir grâce au théorème central limite la variable Z centrée réduite telle que

Z =   =        

  

     .

3.1.2.2           Application et Décision

 

 

           

            ·   si  e_obs > e_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : l’échantillon appartient à une population d’espérance m et n’est pas représentatif de la population de référance d’espérance m₀ .

·   si  e_obs £ e_seuil  l’hypothèse H₀ est acceptée: l’échantillon est représentatif de la population de référence d’espérance m₀.

 

Exemple :   La glycémie d’une population suit une loi normale d’espérance m0 = 1g/l et d’écart-type s0 =  0,1 g/l. On relève les glycémies chez 9 patients. On trouve  = 1,12g/l. Cet échantillon est-il représentatif de la population ? Réponse.

 

 

3.1.3  Variance de la population inconnue

 

3.1.3.1  Statistique du test

La démarche est la même que pour le test e  mais la variance de la population n’étant pas connue, elle est estimée par :

                                            (voir estimation ponctuelle)

 

La statistique étudiée est l’écart : S =  - m₀  dont la distribution de probabilité est la suivante

S ® N (0,  )     avec    E(S) = 0  et   V(S) =     (voir démonstration)

Nous pouvons établir grâce au théorème central limite la variable T centrée réduite telle que

T  =   =        

 

 

3.1.3.2  Application et Décision

           

            ·   si  t_obs > t_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : l’échantillon appartient à une population d’espérance m et n’est pas représentatif de la population de référence d’espérance m₀ .

·   si  t_obs £ t_seuil  l’hypothèse H₀ est acceptée: l’échantillon est représentatif de la population de référence d’espérance m₀.

Remarque : Si n < 30, la variable aléatoire X étudiée doit impérativement suivre une loi normale N(m,s). Pour  n ³ 30, la variable de student t converge vers une loi normale centrée réduite e.

 

Exemple :

Pour étudier un lot de fabrication de comprimés, on prélève au hasard 10 comprimés parmis les 30 000 produits et on les pèse. On observe les valeurs de poids en grammes :

                                          0,81 – 0,84 – 0,83 – 0,80 – 0,85 – 0,86 – 0,85 – 0,83 – 0,84 – 0,80

Le poids moyen observé est-il compatible avec la valeur 0,83g, moyenne de la production au seuil 98% ? Réponse.

 

3.2       Comparaison d’une fréquence observée et une fréquence théorique

3.2.1  Principe du test

Soit X une variable qualitative prenant deux modalités (succès X=1, échec X=0) observée sur une population et un échantillon extrait de cette population.

     

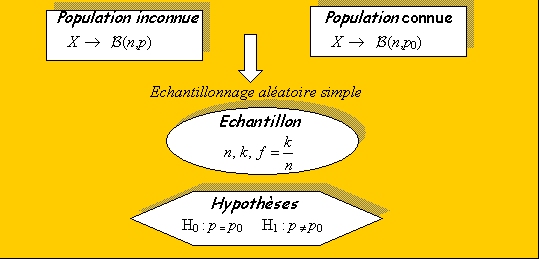
Le but est de savoir si un échantillon de fréquence observée , estimateur de p, appartient à une population de référence connue de fréquence  p₀ (H₀ vraie) ou à une autre population inconnue de fréquence p (H₁ vraie).

 

3.2.2  Statistique du test

La distribution d’échantillonnage de la fréquence de succès dans la population inconnue,   suit une loi normale telle que :  suit  N (p,  ), les variances étant supposées égales dans la population de référence et la population d’où est extrait l’échantillon.

La statistique étudiée est l’écart : S =  – p₀  dont la distribution de probabilité est la suivante S ® N (0,  )     avec  sous H₀  E(S) = 0  et   V(S) =     (voir démonstration)

Nous pouvons établir grâce au théorème central limite la variable Z centrée réduite telle que

                        Z =  =    mais seulement si  np₀ et nq₀  ³ 10 (convergence)

   

        .

3.2.3 Application et décision

           

            ·   si  e_obs > e_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : l’échantillon appartient à une population de fréquence p et n’est pas représentatif de la population de référence de fréquence p₀ .

·   si  e_obs £ e_seuil  l’hypothèse H₀ est acceptée: l’échantillon est représentatif de la population de référence de fréquence p₀.

 

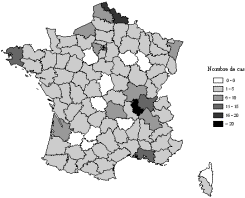
Exemple : Une anomalie génétique touche en France 1/1000 des individus. On a constaté dans une région donnée : 57 personnes atteintes sur 50 000 naissances. Cette région est-elle représentative de la France entière ? Réponse.