 |
 |
Par définition, les variables aléatoires discrètes prennent des valeurs entières discontinues sur un intervalle donné. Ce sont généralement le résultat de dénombrement.
Une distribution de probabilité suit une loi uniforme lorsque toutes les valeurs prises par la variable aléatoire sont équiprobables. Si n est le nombre de valeurs différentes prises par la variable aléatoire, " i, P(X = xi) =
Exemple :
La distribution des chiffres obtenus au lancer de dé (si ce dernier est non pipé) suit une loi uniforme dont la loi de probabilité est la suivante :
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X = xi) |
|
|
|
|
|
|
avec pour espérance : et pour variance
où les valeurs correspondent au rang i de la variable X dans la série.
Dans le cas particulier d’une loi discrète uniforme où les valeurs de la variable aléatoire
X correspondent au rang = i (" i Î [1, n])
et Démonstration.
Soit un univers W constitué de deux éventualités, S pour succès et E pour échec
W = {E, S}
sur lequel on construit une variable aléatoire discrète, « nombre de succès » telle que au cours d’une épreuve, si S est réalisé, X = 1
si E est réalisé, X = 0
On appelle variable de Bernoulli ou variable indicatrice,
la variable aléatoire X telle que : X : W ® R
X (W) = {0,1}
La loi de probabilité associée à la variable de Bernoulli X telle que,
P(X = 0) = q
P(X =1) = p avec p+q = 1
est appelée loi de Bernoulli notée B(1, p)
L’espérance de la variable de Bernoulli est
E(X) = p
car par définition E(X) = = (0 x q) + (1 x p) = p
La variance de la variable de Bernoulli est
V(X) = pq
car par définition V(X) = - E(X)2 = [(0 x q) + (1 x p)] – p2
d’où V(X) = p – p2 = p (1 – p) = pq
Décrite pour la première fois par Isaac Newton en 1676 et démontrée pour la première fois par le mathématicien suisse Jacob Bernoulli en 1713, la loi binomiale est l’une des distributions de probabilité les plus fréquemment rencontrées en statistique appliquée.
Soit l’application Sn : Wn ® Rn
avec Sn = X1 + X2 +…+ Xi + ...+ Xn où Xi est une variable de Bernoulli
La variable binomiale, Sn , représente le nombre de succès obtenus lors de la répétition de n épreuves identiques et indépendantes, chaque épreuve ne pouvant donner que deux résultats possibles.
Ainsi la loi de probabilité suivie par la somme de n variables de Bernoulli où la probabilité associée au succès est p, est la loi binomiale de paramètres n et p.
Sn : Wn ® Rn
® B(n,p)
La probabilité que Sn = k, c’est à dire l’obtention de k succès au cours de n épreuves indépendantes est :
Il est facile de démontrer que l’on a bien une loi de probabilité car :
car p+q = 1
| Remarque : | Le développement du binôme de Newton (p+q)n permet d’obtenir l’ensemble des probabilités pour une distribution binomiale avec une valeur n et p donnée. |
| Il existe également des tables de la loi binomiale où les probabilités sont tabulées pour des valeurs n et p données. |
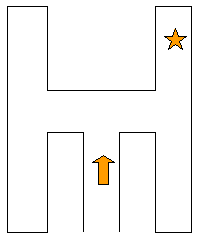
Dans une expérience sur le comportement du rat, rattus norvegicus, on fait pénétrer successivement n rats dans un labyrinthe en forme de H. On étudie alors la probabilité que k rats empruntent la branche supérieure droite du H (voir schéma ci-dessous).
 |
 |
A chaque épreuve, deux évènements peuvent se produire : soit le rat suit l’itinéraire voulu (succès) soit il ne l’emprunte pas (échec). Sachant qu’il y a 4 itinéraires possibles (branches), la probabilité du succès p = 1/4.
Hypothèse :
- si les rats n’ont pas été conditionnés,
- si la branche supérieure droite ne comporte aucun élément attractif ou répulsif,
- si le choix de l’itinéraire d’un rat n’affecte pas le choix du suivant (odeurs)
alors : la variable alé
atoire X « itinéraire emprunté pour x rats » suit une loi binomial
dont la distribution des probabilités est la suivante si l’on étudie le comportement de 5 rats :
|
|
k 0 1 2 3 4 5 |
P(X = k) = 0,237 = 0,395 = 0,264 = 0,088 = 0,015 = 0,001 |
| Remarque : | .Il est possible d’obtenir aisément les valeurs des combinaisons de la loi binomiale en utilisant le triangle de Pascal. |
| De plus on vérifie que la somme des probabilités est bien égale à 1. |
L’espérance d’une variable binomiale Sn est égale à
E(Sn) = np
en effet E(Sn) = E(X1 + X2 +…+ Xi + ...+ Xn )
or E(X1 + X2 +…+ Xi + ...+ Xn ) = propriété de l’espérance
et E(Sn) = avec E(Xi ) = p variable de Bernoulli
d’où E(Sn) = np
La variance d’une variable binomiale Sn est égale à
V(Sn) = npq
en effet V(Sn) = V(X1 + X2 +…+ Xi + ...+ Xn )
or V(X1 + X2 +…+ Xi + ...+ Xn ) = propriété de la variance
et V(Sn) = avec V(Xi ) = pq car variable de Bernoulli
d’où V(Sn) = npq
Exemple :
Dans le cadre de l’étude de comportement du rat , quel est en moyenne le nombre attendu de rats qui vont emprunter l’itinéraire prévu si l’expérience porte sur un lot de 20 rats ? Donnez également la variance et l’écart type de cette variable ? Réponse
La loi binomiale dépend des deux paramètres n et p. Elle est symétrique pour p = 0,5 et dissymétrique pour les autres valeurs de p. La dissymétrie est d’autant plus forte :
(1) pour n fixe, que p est différent de q (graphe)
(2) pour p fixe que n est plus petit.
Afin de faciliter les calculs des probabilités, il est possible d’utiliser une formule de récurrence donnant les valeurs des probabilités successives :
Théorème :
Si Sn et Sm sont deux variables indépendantes suivant des lois binomiales respectivement
Sn ® B(n,p) et Sm ® B(m,p) alors Sn + Sm ® B(n+m,p) démonstration
La loi de Poisson découverte au début du XIXe siècle par le magistrat français Siméon-Denis Poisson s’applique souvent aux phénomènes accidentels où la probabilité p est très faible
(p < 0,05). Elle peut également dans certaines conditions être définie comme limite d’une loi binomiale.
Lorsque n devient grand, le calcul des probabilités d’une loi binomiale
devient très fastidieux. On va donc, sous certaines conditions, trouver une approximation de pk plus maniable.
Comportement asymptotique :
si n ® ¥ et p ® 0,
alors X : B(n,p) ® P(l) avec np ® l (voir démonstration)
| Remarque : | .Cette approximation est correcte si n ³ 50 et np £ 5. |
Exemple :
Soit une loi binomiale de paramètres (100 ; 0,01), les valeurs des probabilités pour k de 0 à 5 ainsi que leur approximation à 10-3 avec une loi de Poisson de paramètre (l= np =1) sont données dans le tableau ci-dessous :
k |
0 1 2 3 4 5 |
|
P(X=k) Approximation |
0,366 0,370 0,185 0,061 0,015 0,000 0,368 0,368 0,184 0,061 0,015 0,003 |
Dans le cas de cet exemple où n =100 et np =1, l’approximation de la loi binomiale par une loi de poisson donne des valeurs de probabilités identiques à 10-3 près.
On appelle processus poissonnien (ou processus de Poisson), le modèle probabiliste des situations qui voient un flux d’évènements se produire les uns à la suite des autres de façon aléatoire (dans le temps et dans l’espace), obéissant aux conditions suivantes :
- la probabilité de réalisation de l’évènement au cours d’une petite période ou sur une petite portion d’espace Dt est proportionnelle à Dt soit pDt .
- elle est indépendante de ce qui s’est produit antérieurement ou à côté,
- la probabilité de deux apparitions sur le même Dt est négligeable.
Ainsi, des évènements qui se réalisent de façon aléatoire comme des pannes de machines, des accidents d’avions, des fautes dans un texte, …peuvent être considérés comme relevant d’un processus poissonnien.
Une variable aléatoire X à valeurs dans R suit une loi de Poisson de paramètre l (l > 0) si les réels pk sont donnés par
on note : X ® P(l)
| Remarque : | .Une loi de Poisson est donnée par sa loi de probabilité : |
|
(1) "k, P(X = k) > 0 (2) or d’où |
Exemple :
|
Une suspension bactérienne contient 5000 bactéries/litre. On ensemence à partir de cette suspension, 50 boites de Pétri, à raison d’1 cm3 par boite. Si X représente le nombre de colonies par boite, alors la loi de probabilité de X est : X ® P (l=5) |
Boite de Pétri avec colonies bactériennes |
La probabilité qu’il n’y ait aucune colonie sur la boite de Pétri est :
0,0067 soit approximativement 0,67 % de chance.
La probabilité qu’il n’y ait au moins une colonie sur la boite de Pétri est :
P(X > 0)=1- P(X = 0) = 1-0,0067 = 0,9933 soit 99,3 % de chance d’avoir au moins une colonie bactérienne qui se développe dans la boite de Pétri. (voir événement contraire)
Comme pour la loi binomiale, il est possible d’utiliser une formule de récurrence pour calculer les valeurs des probabilités successives :
L’espérance d’une variable aléatoire de Poisson est
E(X) = l
Par définition avec k Î N valeurs prises par la v.a. X
avec
d’où
La variance d’une variable de Poisson est
V(X) = l
Par définition
en posant , alors
d’où
d’où
d’où
| Remarque : | .Il est à noter que dans le cas d’une variable aléatoire de Poisson, l’espérance et la variance prennent la même valeur. |
| Ceci est un élément à prendre en compte lors des tests d’ajustement à une loi de probabilité. |
Exemples :
(1) Dans le cadre de la culture bactérienne, le nombre moyen de colonies attendu sur la boite de Pétri est : E(X) = l = 5 colonies.
Ainsi si l’on effectue plusieurs cultures bactériennes (plusieurs boites de Pétri) à partir de la même solution initiale, on attend en moyenne cinq colonies pour l’ensemble des boites.
En ce qui concerne la variance et l’écart-type , on aura :
V(X) = l = 5 et 2,24 colonies.
(2) Sachant que 0,2 % des sujets présentent une allergie lors d’une vaccination, quelles sont les valeurs de l’espérance et de la variance du nombre de sujets atteints lors d’une campagne de vaccination concernant 1000 sujets ? Réponse.
Si X et Y sont deux variables aléatoires indépendantes suivant des lois de Poisson respectivement
X ® P (l) et Y ® P (m) alors X + Y® P (l+m) démonstration
Sous le schéma de Bernoulli (épreuves identiques et indépendantes), on désire obtenir n succès et l’on considère la variable aléatoire discrète X qui représente le nombre d’épreuves indépendantes k nécessaire à l’obtention des n succès.
X suit une loi binomiale négative de paramètres n et p notée BN (n,p) si :
avec k, n Î N et k ³ n
| Remarque : | .Dans le cas de la loi binomiale négative, le nombre de succès n est connu et l’on cherche le nombre d’épreuves k, nécessaire pour obtenir les n succès. |
| Ainsi le dernier évènement est connu car les épreuves cessent avec l’obtention du
nième succès et l’on choisit
n-1 objets parmi k-1. |
Exemple :
Pour étudier le domaine vital d’une population de poissons, des émetteurs radio sont fixés au niveau de la nageoire dorsale après une légère anesthésie locale. Suite à divers aléas, on considère que 30 % des poissons équipés ne sont pas repérés par la suite. Si l’on considère qu’un minimum de 15 poissons doivent être suivis pour avoir des résultats statistiquement acceptables, la variable aléatoire X « nombre de poissons devant être équipés » suit une loi binomiale négative X ® BN (15, 0,70)
En posant comme hypothèse que les causes de pertes de liaisons radio soient suffisamment nombreuses pour assurer l’indépendance entre chaque épreuve, la probabilité d’être obligé d’équiper 20 poissons est de :
0,13
L’espérance associée à une loi binomiale négative est :
La variance associée à une loi binomiale négative est :
Lorsque le nombre de succès n est égal à 1, la loi de la variable aléatoire discrète X porte le nom de loi de Pascal ou loi géométrique de paramètre p telle que :
P(X = k) = pqk-1 avec k Î N*
|
Voici pourquoi : Si l’on considère la variable aléatoire X « nombre de naissances observées avant l’obtention d’une fille » avec p = 1/2 (même probabilité de naissance d’une fille ou d’un garçon), la loi suivit par X est une loi géométrique car : X = 1 si {X= F} avec P(X = 1) = p X = 2 si {X= GÇF} avec P(X = 2) = qp X = 3 si {X= GÇGÇF} avec P(X = 3) = qqp = q2p d’où X = k si {X=GÇGÇ…Ç.GÇF} avec k-1 {X=G} et donc P(X = k) = pqk-1 |
D’où l’espérance associée à la loi géométrique est :
et la variance associée à la loi géométrique est :
Exemple :
Lors de la traduction d’un ARN messager en polypeptide (suite d’acides aminés), l’arrêt dans l‘élongation du polypeptide est lié à l’apparition d’un codon terminateur ou codon stop au niveau de l’ARN messager. Si l’on considère la variable aléatoire X « nombre d’acides aminés associés avant l’apparition d’un codon stop », quelle est la longueur moyenne d’une protéine attendue ? Réponse