Chapitre 7 : Tests d’hypothèse

4         Tests d’homogénéité

 

Les tests d’homogénéité ou d’égalité destinés à comparer deux populations à l’aide d’un nombre équivalent d’échantillons sont les plus couramment utilisés. Dans ce cas la loi théorique du paramètre étudié (par exemple p, m , s² )  est inconnue au niveau des populations étudiées.

 

4.1         Comparaison de deux variances

4.1.1  Principe du test

Soit X, une variable aléatoire observée sur 2 populations suivant une loi normale et deux échantillons indépendants extraits de ces deux populations.

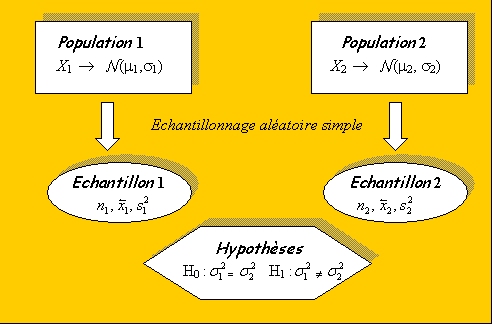
On fait l’hypothèse que les deux échantillons proviennent de 2 populations dont les variances sont égales.

Le test de comparaison de variance est nécessaire lors de la comparaison de deux moyennes lorsque les variances des populations  et  ne sont pas connues. C’est également la statistique associée à l’analyse de variance.

 

4.1.2  Statistique du test

La statistique associée au test de comparaison de deux variances correspond au rapport des deux variances estimées.

 

 

 

4.1.3. Application et Décision

La valeur de la statistique F calculée (F_obs) est comparée avec la valeur F_seuil  lue dans la table de la loi de Fisher-Snedecor pour un risque d’erreur a fixé et (n₁-1, n₂ -1) degrés de liberté.

 

            ·   si  F_obs > F_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : les deux échantillons sont extraits de deux populations ayant des variances statistiquement différentes  et .

·   si  F_obs £ F_seuil  l’hypothèse H₀ est acceptée: les deux échantillons sont extraits de deux populations ayant même variance .

Remarque :	Pour l’application de ce test, il est impératif que X ®  N(m,s) et que les deux échantillons soient indépendants.

 

 

Exemple : Un biologiste effectue des dosages par une méthode de mesure de radioactivité et ne dispose donc que d’un nombre très limité de valeurs. Les concentrations C1 et C2 mesurées sur deux prélèvements ont donné les valeurs suivantes : C1 : 3,9 – 3,8 – 4,1 – 3,6            C2 : 3,9 – 2,8 – 3,1 – 3,7 – 4,1 La variabilité des valeurs obtenues pour les deux prélèvements est-elle similaire ? Réponse.

 

 

4.2       Comparaison de deux moyennes

4.2.1  Principe du test

Soit X un caractère quantitatif continu observé sur 2 populations suivant une loi normale et deux échantillons indépendants extraits de ces deux populations.

    

 

 

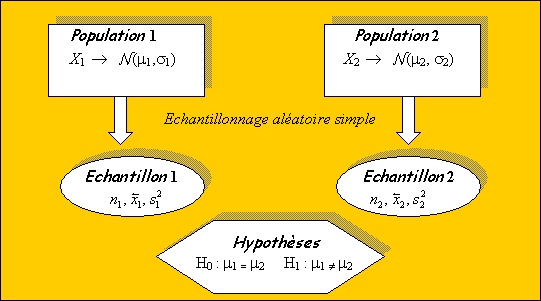
On fait l’hypothèse que les deux échantillons proviennent de 2 populations dont les espérances sont égales.                                                 

Il existe plusieurs statistiques associées à la comparaison de deux moyennes en fonction de la nature des données.

 

                                                                                                                        

 

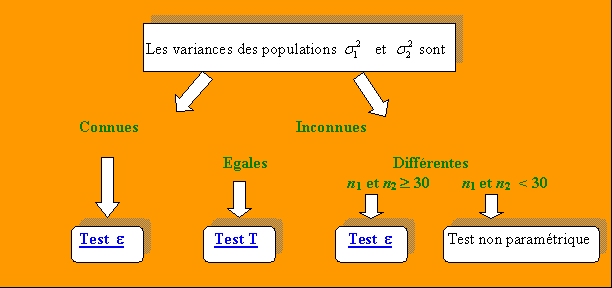
4.2.2  Les variances des populations sont connues

 

4.2.2.1  Statistique du test

 

·   Soit  la distribution d’échantillonnage de la moyenne dans la population 1  suit une loi normale telle que :   ®  N (m₁,  )   et    de même pour         ®  N (m₂,  )

·    et  étant deux variables aléatoires indépendantes, nous pouvons établir la loi de probabilité de la variable aléatoire à étudier

                      E(  ) = E(  ) - E(  ) = m₁ - m₂               (Propriété de l’ espérance)

                               V(  ) = V(  ) - V(  ) =  +           (Propriété de la variance)

·   Sachant que  suit une loi normale N(m₁ - m_{2 ,  ,} nous pouvons établir grâce au théorème central limite la variable Z centrée réduite telle que

               Z =  =  

 

        .

 

4.2.2.2  Application et décision

 

            ·   si  e_obs ³ e_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : les deux échantillons sont extraits de deux populations ayant des espérances respectivement m₁ et m₂.

·   si  e_obs £ e_seuil  l’hypothèse H₀ est acceptée: les deux échantillons sont extraits de deux populations ayant même espérance m.

Remarque :	Pour l’application de ce test, il est impératif que X ® N(m,s) pour les échantillons  de taille < 30 et  que les deux échantillons soient indépendants.

Exemple :

 

On a effectué une étude, en milieu urbain et en milieu rural, sur le rythme cardiaque humain :

Effectif de l’échantillon	300	240
Moyenne de l’échantillon	80	77
Variance de la population	150	120

 

Peut-on affirmer qu’il existe une différence significative entre les rythmes cardiaques moyens des deux populations ? Réponse.

 

4.2.3   Les variances des populations  sont inconnues et égales

 

4.2.3.1  Statistique du test

 

· Les variances des populations n’étant pas connues, on fait l’hypothèse que les deux populations présentent la même variance.

            H₀ :  =  = s²                    (voir test de comparaison des variances)

· L’égalité des variances des deux populations ou homoscédasticité permet alors d’établir la loi de probabilité de  avec

       ®  N (m₁,  ) et  ®  N (m₁,  )

·   Sachant que  suit une loi normale N(m₁ - m_{2 , ,} nous pouvons établir grâce au théorème central limite la variable T telle que

            T =  =  

 

 

 

4.2.3.2  Application et décision

 

 

·   si  t_obs > t_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : les deux échantillons sont extraits de deux populations ayant des espérances respectivement m₁ et m₂.

·   si  t_obs £ t_seuil  l’hypothèse H₀ est acceptée: les deux échantillons sont extraits de deux populations ayant même espérance m.

Remarque :	PoPour l’application de ce test, il est impératif que X ® N(m,s) pour les échantillons de taille < 30,
	que les deux échantillons soient indépendants et que les deux variances estimées soient égales.

 

Exemple :

Dans le but d’étudier l’influence du type d’atmosphère d’élevage sur la durée de développement des drosophiles femelles, ces dernières ont été élevées à 14°C sous atmosphère normale (N) ou enrichie en C0₂ (C02). Les résultats suivants ont été obtenus :

 

	N	864, 768, 912, 804, 924, 984, 888, 816, 840, 936, 792, 876
	C02	840, 948, 936, 1032, 912, 948, 1020, 936, 1056, 876, 1032, 918

 

Que peut-on conclure ? Réponse. 

 

4.2.4  Les variances des populations sont inconnues et inégales

 

Si les variances des populations ne sont pas connues et si leurs estimations à partir des échantillons sont significativement différentes ( test de comparaison des variances), il faut considérer deux cas de figure selon la taille des échantillons comparés :

 

les grands échantillons avec n₁ et n₂ supérieurs à  30.

les petits échantillons avec n₁ et/ou n₂ inférieurs à  30.

 

Cas où n₁ et n₂ ³ 30

 

La statistique utilisée est la même que pour le cas où les variances sont connues.

 

Comme les variances sont inconnues et significativement différentes  ¹ , on remplace les variances des populations par leurs estimations ponctuelles calculées à partir des échantillons,

                                           et    

           

           ·   si  e_obs > e_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : les deux échantillons sont extraits de deux populations ayant des espérances respectivement m₁ et m₂.

·   si  e_obs £ e_seuil  l’hypothèse H₀ est acceptée: les deux échantillons sont extraits de deux populations ayant même espérance m.

Remarque :	Pour l’application de ce test, il est impératif que les deux échantillons soient indépendants.

Exemple :

Dans le but d’étudier l’influence éventuelle de la lumière sur la croissance du poisson Lebistes Reticulus, on a élevé deux lots de ce poisson dans des conditions d’éclairage différentes. Au 95^ème jour, on a mesuré en mm les longueurs x_i des poissons. On a obtenu les résultats suivants : 

Lot 1 (180 individus) : éclairage à 400 lux                     = 3 780             = 84 884

Lot 2 (90 individus) : éclairage à 3 000 lux.              = 2 043                  = 46 586

Que peut-on conclure ? Réponse. 

 

Cas où n₁ et/ou  n₂ < 30

 

Lorsque les variances sont inégales et les échantillons de petites tailles, la loi de probabilité suivie par  n’est pas connue. On a recours alors au statistique non paramétrique.

 

4.3       Comparaison de deux fréquences

4.3.1  Principe du test

Soit X une variable qualitative prenant deux modalités (succès X=1, échec X=0) observée sur 2 populations et deux échantillons indépendants extraits de ces deux populations. On fait l’hypothèse que les deux échantillons proviennent de 2 populations dont les probabilités de succès sont identiques.                           

  

 

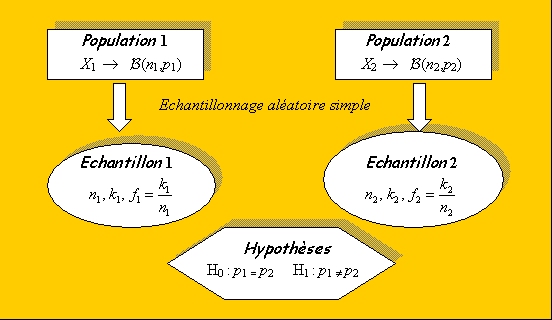
Le problème est de savoir si la différence entre les deux fréquences observées est réelle ou explicable par les fluctuations d’échantillonnage. Pour résoudre ce problème, deux tests de comparaison de fréquences sont possibles :

            Test e ou test de la variable centrée réduite et test du Khi-deux c²

 

4.3.2 Statistique du test e

·  La distribution d’échantillonnage de la fréquence de succès dans la population 1,   suit une loi normale telle que :

            suit  N (p₁,  )  et de même pour  suit  N (p₂,  ) 

si et seulement si n₁p₁, n₁q₁, n₂p₂, n₂q₂  > 10

·    et   étant deux variables aléatoires indépendantes, nous pouvons établir la loi de probabilité de la variable aléatoire à étudier

                    E(  ) = E(  ) - E(  ) = p₁ - p₂                             (Propriété de l’ espérance)

                           V(  ) = V(  ) + V(  ) =  +          (Propriété de la variance)

·   Sachant que  suit une loi normale N(p₁ - p_{2 , ,} nous pouvons établir grâce au théorème central limite la variable Z centrée réduite telle que

                                     Z =                    

 

4.3.3 Application et décision

La valeur p, probabilité du succès commune aux deux populations n’est en réalité pas connue. On l’estime à partir des résultats observés sur les deux échantillons :

                         où k₁ et k₂ représentent le nombre de succès observés respectivement pour l’échantillon 1 et pour l’échantillon 2.

 

 

            ·   si  e_obs > e_seuil  l’hypothèse H₀ est rejetée au risque d’erreur a : les deux échantillons sont extraits de deux populations ayant des probabilités de succès  respectivement p₁ et p₂.

·  si  e_obs £ e_seuil  l’hypothèse H₀ est acceptée: les deux échantillons sont extraits de deux populations ayant même probabilité de succès p.

 

Exemple :

On veut tester l’impact des travaux dirigés dans la réussite à l’examen de statistique.

	Groupe 1	Groupe 2
Nbre d’heures de TD	20 h	30 h
Nbre d’étudiants	180	150
Nbre d’étudiants ayant réussi à l’examen	126	129

 

Qu’en concluez-vous ? Réponse.